网络的可靠性参数

⚠ 转载请注明出处：作者：ZobinHuang，更新日期：Mar.16 2022

    本作品由 ZobinHuang 采用 知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议 进行许可，在进行使用或分享前请查看权限要求。若发现侵权行为，会采取法律手段维护作者正当合法权益，谢谢配合。

目录

有特定需要的内容直接跳转到相关章节查看即可。

正在加载目录...

连通度

点割的定义

    给定连通图 `G`, 设 `V' \subseteq V(G)` , 若 `G−V’` 不连通, 称 `V’` 为 `G`的一个 (顶)点割 (Vertex Cut)，包含 `k` 个顶点的点割称为 k 点割(k-cut)。`G` 中点数最少的点割称为 最小点割 (Minimum Vertex Cut)。

    如上图所示，在 `G_1` 中，`{v_3}`, `{v_3,v_5}` 等都是点割; 而在 `G_2` 中，我们找不到点割 (i.e. 不论怎么删点，`G` 都是一个连通图)。

    值得注意的是，上一篇文章中介绍的 割点 是点割的一种特殊情形。

    另外，完全图一定不存在点割。

边割的定义

    同理，给定连通图 `G`, 设 `E' \subseteq E(G)` , 若 `G−E’` 不连通, 则称 `E’` 为 `G` 的 一个 边割 (Edge Cut)，包含 `k` 条边的边割称为 k 边割 (k-edge Cut)。`G` 中包含边数最少的边割称为 最小边割 (Minimum Edge Cut)。

    还是同样的例子，在 `G_1` 中，`{v_1v_2}`, `{v_1v_3}` 等都是边割; 在 `G_2` 中，与 `v_1` 关联的所有边 `{v_1v_2, v_1v_3, v_1v_4}` 构成了图 `G_2` 的最小边割。

    与点割不同，非平凡连通图一定存在边割。

点连通度 和 边连通度 的定义

    在 `G` 中, 若存在点割, 则称 `G` 的最小点割的顶点数为 `G` 的 (点)连通度 (Connectivity), 记为 `\kappa(G)`, 简记为 `\kappa`。若不存在点割 (i.e. 完全图)，则称 `n(G)−1` 为其 (点)连通度 (无点割，使得剩余图为孤立点时需删去的顶点数)。若 `G` 不连通, 则 `\kappa(G)=0`。

    在 `G` 中, 最小边割所含边数称为 `G` 的 边连通度 (Edge Connectivity)，边连通度记为 `\lamda(G)`。若 `G` 不连通或 `G` 是平凡图,则定义 `\lamda(G)=0`。

    在 `G` 中, 若 `\kappa(G) \ge k`, 称 `G` 是 `k` 连通的 (k-connected)；若 `\lamda(G) \ge k`, 称 `G` 是 `k` 边连通的 (k-edge-connected)。

    确定一个图 `G`是否 `k` (边)连通的思路是：找是否存在一个 点(边)割 小于 `k` 个点(条边)。计算图的连通度有多项式时间算法，具体可参考 compute_connectivity。计算图的边连通度也有多项式时间的算法，具体可参考 compute_edge_connectivity。

    使用一样的例子，对于 `G_1` 来说，`\kappa(G_1)=1`，`\lamda(G_1)=1`; 对于 `G_2` 来说，`\kappa(G_2)=3`，`\lamda(G_2)=3`。

连通度的性质

    给出定理:

对图 `G` 的任意一个顶点 `v` 和一条边 `e`，有关系式: `\kappa(G)−1 \le \kappa(G−v)`

    证明:

1. 若 `G-v` 不存在点割，则 `\kappa(G-v) = n(G-v)-1 = (n-1)-1 = n-2`。由于有 `\kappa(G) \le n-1`，故有 `\kappa(G-v)+1 = n-1 \ge \kappa(G)`，也即 `\kappa(G)−1 \le \kappa(G−v)`。
2. 若 `G-v` 存在点割，则在 `G-v` 中可以找到一个最小点割，记为 `V_{min}`，故 `G-v-V_{min}` 不连通，也即 `G-V_{min} \cup {v}` 不连通，则 `V_{min} \cup {v}` 是 `G` 的一个点割。由于 `V_{min} \cup {v}` 的大小不会小于最小点割，故 `\kappa(G) \le |V_{min} \cup {v}| = |V_{min}| +|{v}| = kappa(G-v) + 1`。

    下面给出 Whitney 定理：

`\kappa(G) \le \lamda(G) \le \delta(G)`

    证明:

    先证: `\lamda(G) \leq \delta(G)`: 找到图中的 `d(v)=\delta`，删去这个点关联的所有边，则这些边就组成了一个边割。

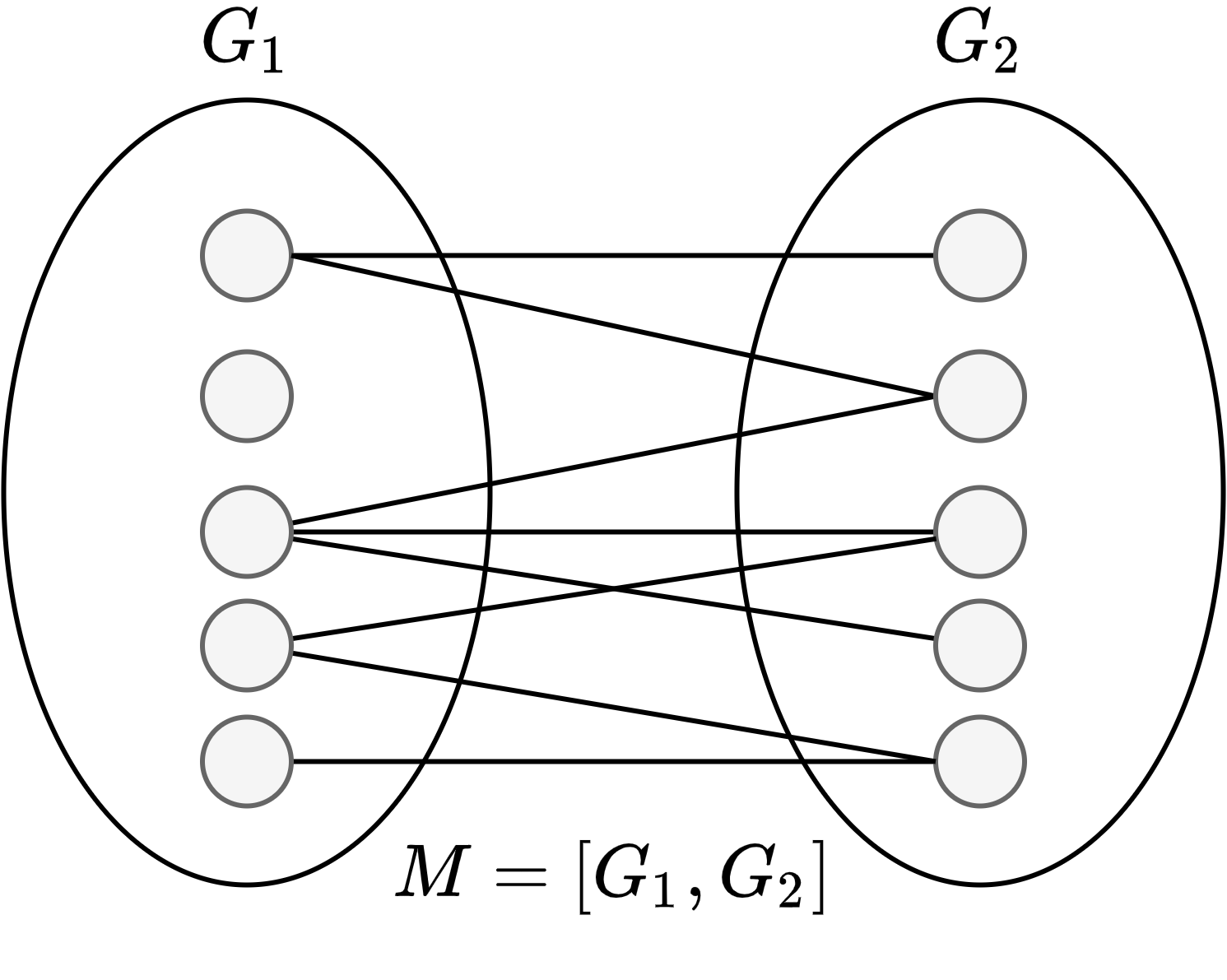
    再证 `\kappa(G) \le \lamda(G)`: 设图的最小边割为 `[S,\bar{S}]`。容易证明 `G-[S,\bar{S}]` 一定包含两个分支，否则 `[S,\bar{S}]` 不是最小边割。我们记 `\lamda(G) = [S,\bar{S}]`。然后我们分两种情形:

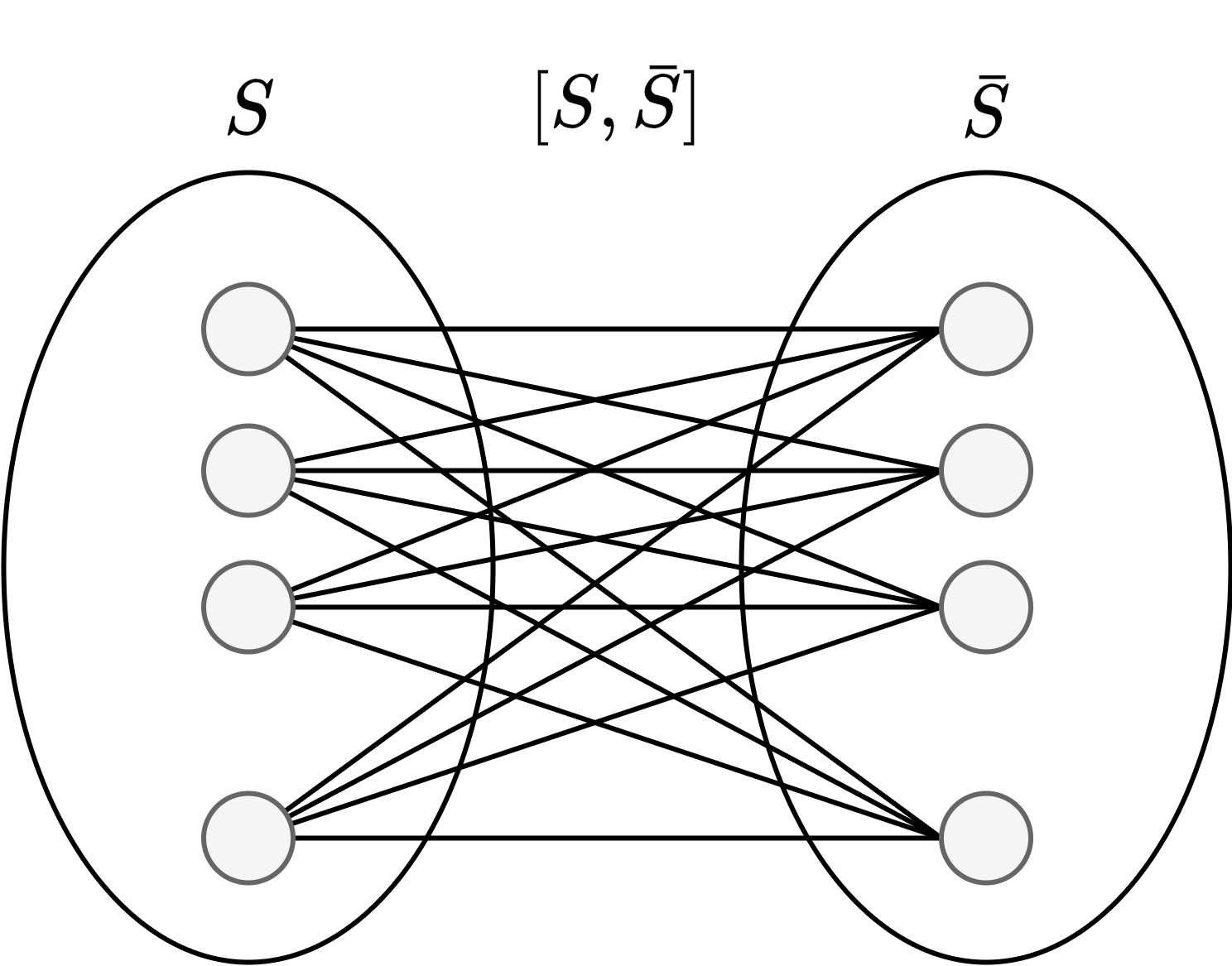
    如上图所示，考虑 `S` 中的点和 `\bar{S}` 中的点均连接的情况，则有 `\lamda(G) = |``[S,\bar{S}]``| = |S|\cdot|\bar{S}|`。由于 `|S|+|\bar{S}|=n`，故 `\lamda(G) = |``[S,\bar{S}]``| = |S|\cdot|\bar{S}| \ge (n-1)\cdot1 = n-1 \ge \kappa(G)`。

    然后考虑 `S` 中的点和 `\bar{S}` 中的点不全相邻的情况。取 `x\inS,y\in\bar{S}` 且 `x` 与 `y` 不相邻的情况。

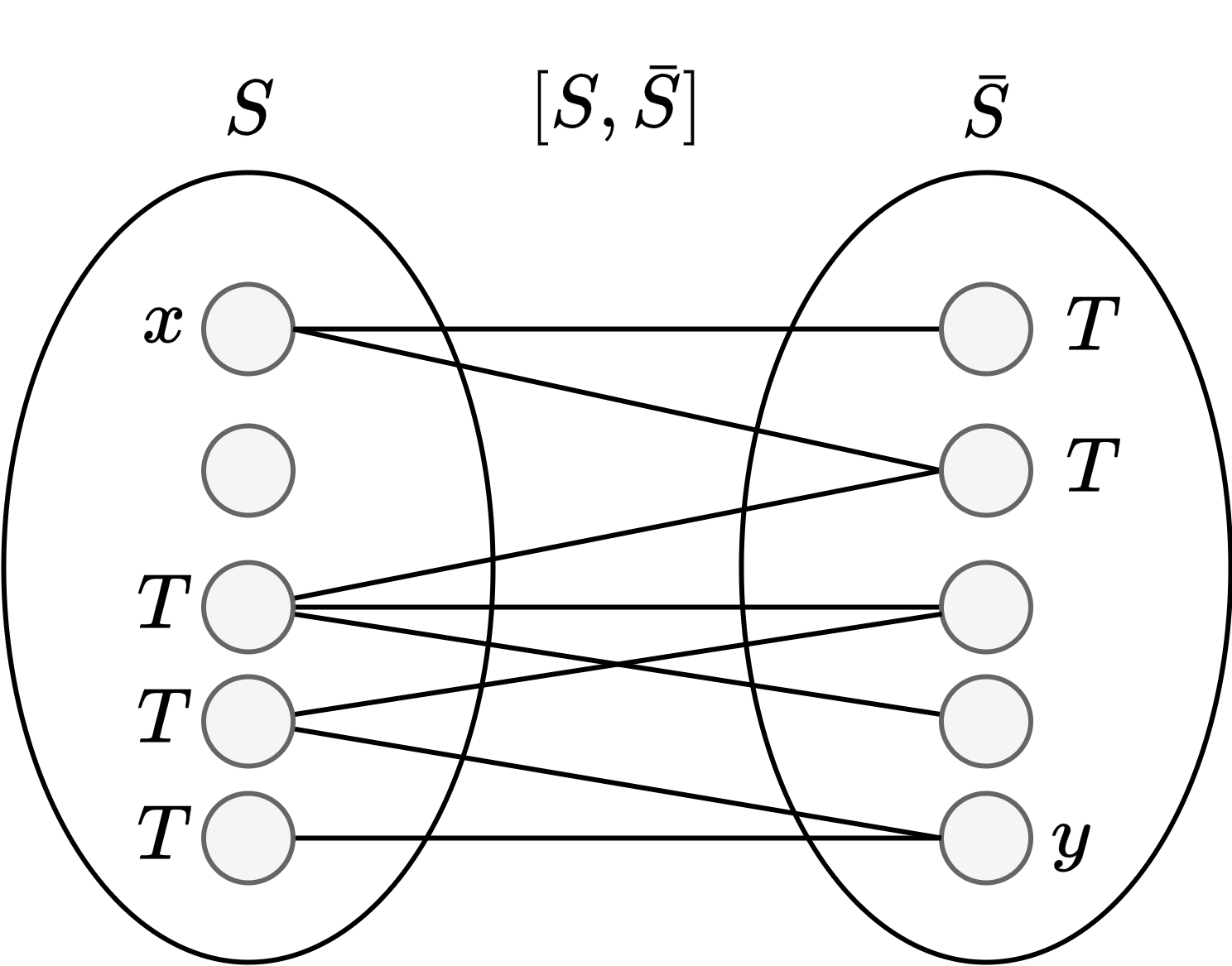
    令 `T = {v|x \leftrightarrow v, 且 v\in\bar{S}} \cup {u|u \ne x, u \in S 且 u 在 \bar{S} 中有邻点}`，如上图所示。所以，在图 `G` 中任意一条 `x`, `y` 路必然经过 `T` 中一些点，所以 `T` 为 `G` 的一个点割。在 `G` 中取如下边集:

`E_1 = {xv|v\in\bar{S}} \cup {从 T \cap S 每个顶点取一条到 \bar{S} 的边}`

    上面的边集如下图所示:

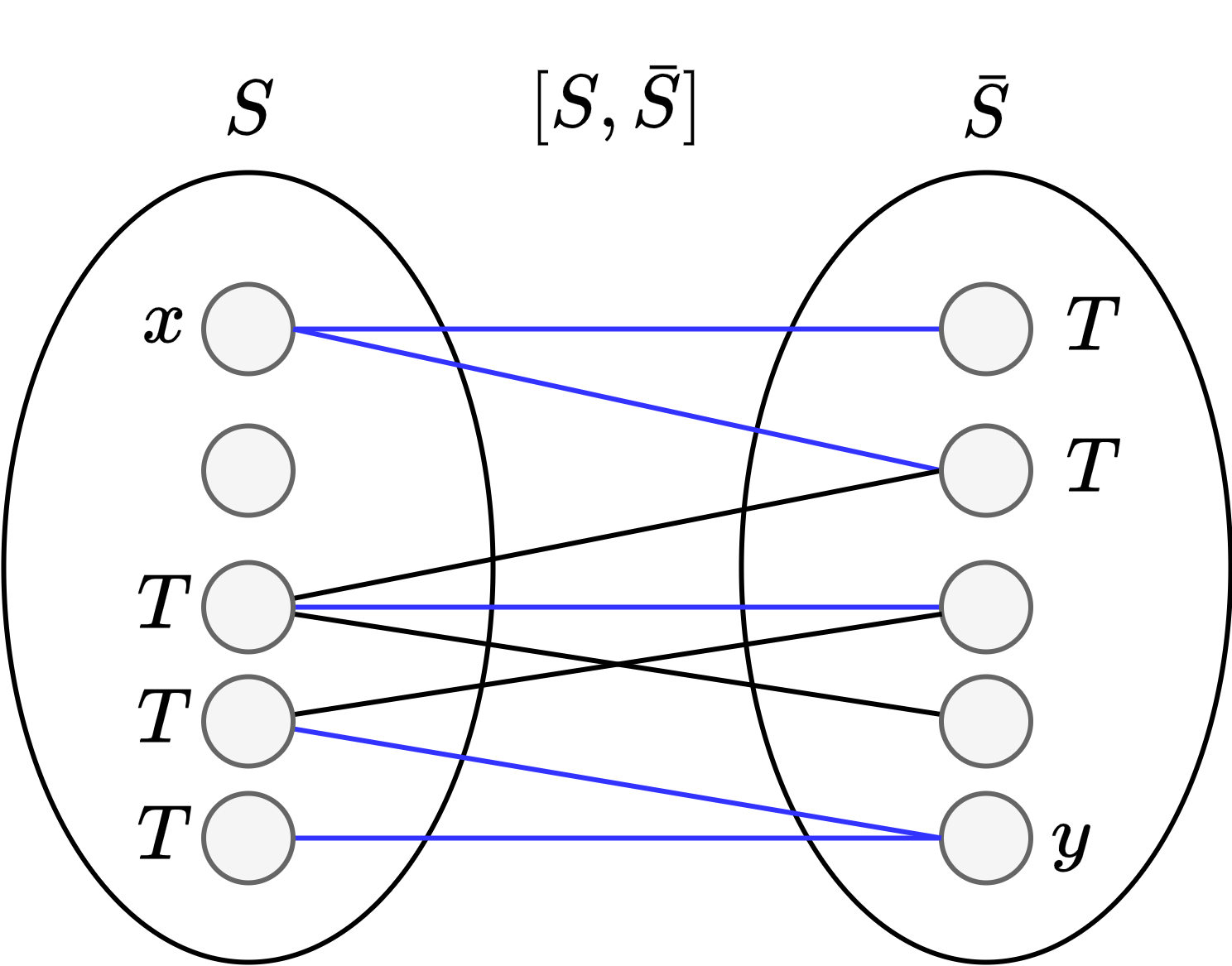
    则我们可以得到: `|E_1|=|T|`，因此 `\lamda(G) = |``[S,\bar{S}]``| \ge |E_1| = |T| \ge \kappa(G)`。

    对于上述不等式，严格不等式 ( i.e. `\kappa(G) < \lamda(G) < \delta(G)` ) 是可以成立的，等式 ( i.e. `\kappa(G) = \lamda(G) = \delta(G)` ) 也是可以成立的。实际上，Chartrand 和 Harary 在 1968 年证明了：

对任意正整数 `0 < a \le b \le c`，都存在图 `G`，使得 `\kappa(G)=a`, `\lamda(G)=b`, `\delta(G)=c`。

用于计算边连通度的定理

    下面我们给出两个与连通度有关的数值关系。

求边连通度: 令 `S` 是图 `G` 的一个非空顶点集, 则: `|``[S,\bar{S}]``|`` = \sum_{v\inS}d(v) - 2E(G[S])`

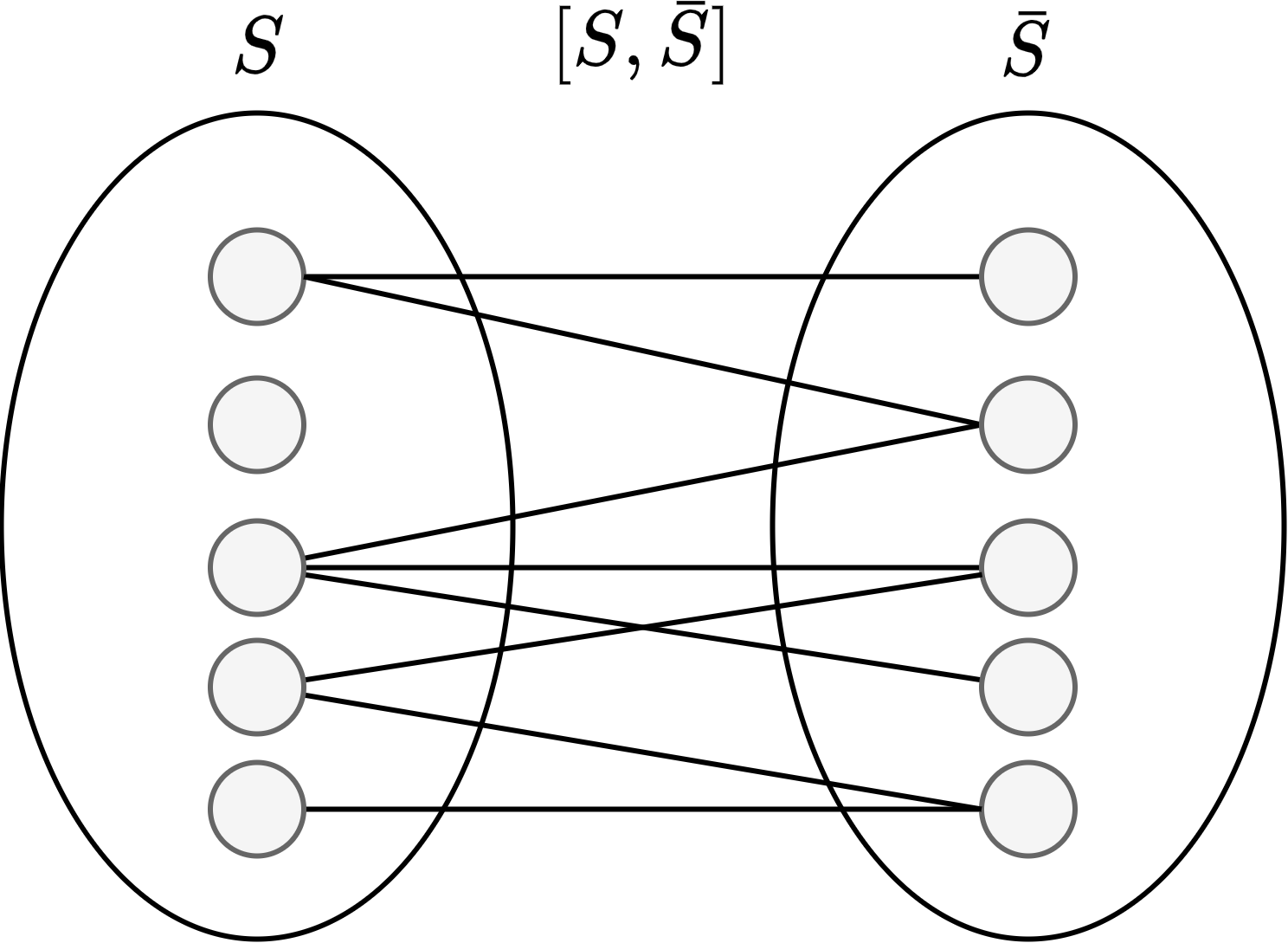
    证明:

    `G[S]` 中的一条边对 `\sum_{v\inS}d(v)` 贡献为 2，而 `[S,\bar{S}]` 中的边仅贡献 1，因此由握手定理可以得到:

`\sum_{v\inS}d(v) = ``|``[S,\bar{S}]``|`` + 2E(G[S])`

求点连通度: 设 `G` 是 `(n,m)` 连通图，则: `\kappa(G) \le \floor{\frac{2m}{n}}`

    证明:

    由握手定理可得，`2m = \sum_{v \in V(G)}d(v) \ge n \cdot \delta(G) \ge n \cdot \kappa(G)`，因此 `\kappa(G) \le \floor{\frac{2m}{n}}`。

哈拉里图

    哈拉里证明了 connectivity_5 中取等号的情况，也即一定存在一个 `(n,m)` 图 `G`，使得 `\kappa(G) = \floor{\frac{2m}{n}}` 成立。

    反过来想，由 Whitney 定理 `\kappa(G) \le \delta(G)` 可知，连通度为 `k` 的图至少包含 `\ceil{\frac{n(G) \cdot \delta(G)}{2}} \ge \ceil{\frac{n(G) \cdot \kappa(G)}{2}}` 条边。如果取等号，则就正好找到了一个连通度为 `k` 且边数正好等于 `\ceil{\frac{n(G) \cdot \kappa(G)}{2}}` 的图。我们把这种图称为 哈拉里图 (Harary Graph)，记为 `H_{k,n}`。

    哈拉里图的物理意义是：当通讯网络线路昂贵时, 用最少的边使得网络达到可能的最大连通度(可靠性)。

    下面我们分情况介绍哈拉里图的作图方法。

    若连通度 `k` 和图的阶数 `n` 都是偶数，我们表示为 `H_{2r,n}`，则我们给每个顶点进行标号，得到 `V(H)={0,1,2,...,n-1}`，然后我们作边的策略是：`E(H)={ij||i-j| \leq r}`，亦即每个顶点都与其最近的 `r` 个顶点连边，举例如下 (i.e. `H_{4,8}`):

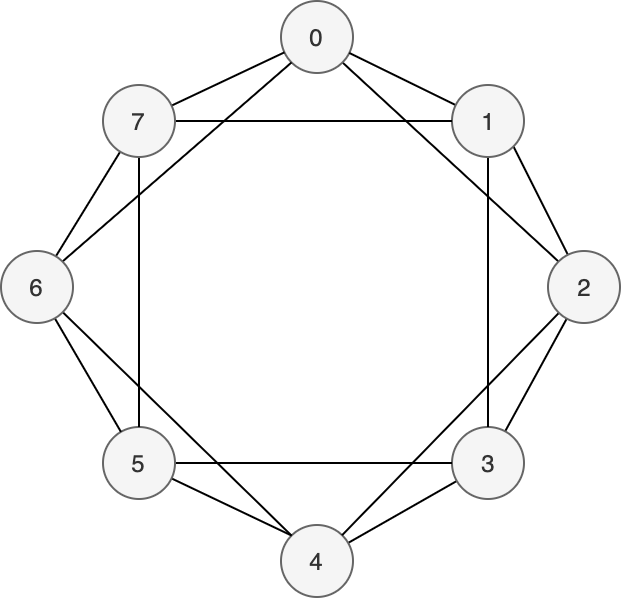
    若连通度 `k` 是奇数，图的阶数 `n` 是偶数，我们表示为 `H_{2r+1,n}`，则我们给每个顶点进行标号，得到 `V(H)={0,1,2,...,n-1}`，然后我们作边的策略是：先作 `H_{2r,n}`，然后对 `i` 与 `i + \frac{n}{2}` (`0 \le i < \frac{n}{2}`) 进行连线，也即首先每个顶点都与其最近的 r 个顶点连边, 然后再加上 对角顶点间的连边。举例如下 (i.e. `H_{5,8}`):

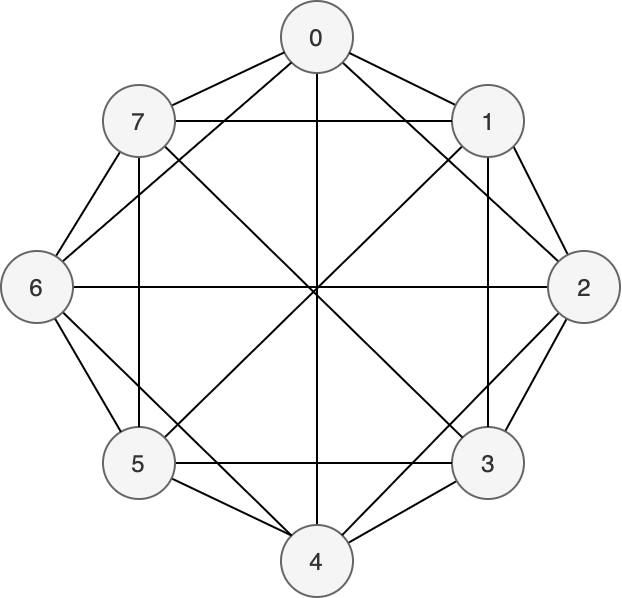
    若连通度 `k` 和图的阶数 `n` 都是奇数，我们表示为 `H_{2r+1,n}`。先作 `H_{2r,n}`，然后对 `i` 与 `i+\frac{n-1}{2}` (`0 \le i \le \frac{n−1}{2}`) 进行连线。举例如下 (i.e. `H_{5,9}`):

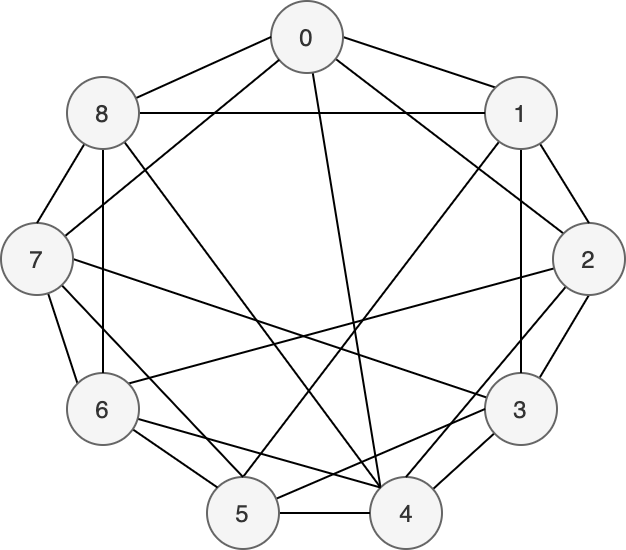
连通度和图的度的关系

    下面我们给出几个关于图的连通度和图的度之间的数值关系。

设 `G` 是 `(n,m)` 简单图，若 `\delta(G) > \floor{\frac{n}{2}}`，则 `G` 连通，且有 `\lamda(G) = \delta(G)`

    证明连通性:

    若 `G` 不连通，则 `G` 至少有两个连通分支。于是至少有一个分支 `H`，使得 `\delta(H) \le \floor{\frac{n}{2}}-1 < \floor{\frac{n}{2}}`，矛盾。

    证明 `\lamda(G) = \delta(G)`:

    若 `\lamda(G) < \delta(G)`，设 `M` 是 `G` 的最小边割, 则 `|M|=\lamda(G)`，且 `G−M` 恰有两个连通分支 `G_1` 和 `G_2`，对 `G_1` 用 connectivity_4 的结论，可得:

`\delta(G) > \lamda(G) = |M| = \sum_{v \in G_1}d(v) - 2|E(G_1)|`

    观察等式右边的两项，我们可以构造以下的不等关系:

`\sum_{v \in G_1}d(v) > \sum_{v \in G_1}\delta(G)`
`2|E(G_1)| \le |V(G_1)| \cdot |V(G_1)-1|`

    故原式可以转化为: `\delta(G) > |V(G_1)|\delta(G) - |V(G_1)| \cdot |V(G_1)-1|`

    由题设关系 `\delta(G) > \floor{\frac{n}{2}}` 可得 `|V(G_1)| > 1`。基于这个关系，我们对上式进行因式分解，可得:

`|V(G_1)|\delta(G) - \delta(G) < |V(G_1)| \cdot |V(G_1)-1|`
`\delta(G) < |V(G_1)|`
`|V(G_1)| \ge \delta(G) + 1`

    同理可得:

`|V(G_2)| \ge \delta(G) + 1`

    注意到 `n = |V(G_1)|+|V(G_2)| \ge 2\delta(G) + 2`，即 `\delta(G) \le \frac{n}{2}-1`，这与题设矛盾。

设 `G` 是 `(n,m)` 简单图，若对于任意正整数 `k`，有 `\delta(G) \ge \frac{n+k-2}{2}`，则 `G` 是 `k` 连通的

    证明:

    任意删去 `k−1` 个顶点, 记所得之图为 `H`，则

`\delta(H) \ge \delta(G)-(k-1) \ge \frac{n+k-2}{2}-(k-1) = \frac{n-k}{2}`

    由于 `\delta(H)` 是整数，故:

`\delta(H) \ge \ceil{\frac{n-k}{2}} = \floor{\frac{n-k+1}{2}}`

    由 connectivity_6 可得，包含 `n-k+1` 个顶点的 `H` 是连通的。

    所以 `G` 是 `k` 连通的 (i.e. 删去 `k-1` 个顶点之后仍然连通，那么最小点割 `\kappa(G) \ge k`)。

描述连通度的其它参数

    对上面三个图进行观察，可以发现 `\kappa(G_1)=\kappa(G_2)=\kappa(G_3)=1`，`\lamda(G_1)=\lamda(G_2)=\lamda(G_3)=1`，但是明显地，这三个图的 "连通性" 是不同的，这说明连通度对图的 "连通性" 的刻画是片面的。因此我们在下面给出另一种描述 "连通性" 的数字量 —— 坚韧度。

坚韧度

    用 `C(G)` 定义为图 `G` 的全体点割构成的集合 (i.e. 其实是一个集族，每一个成员是一个集合)，非平凡非完全图的 坚韧度 (Toughness) 记作 `\tau(G)`，定义如下:

`\tau(G) = min{\frac{|S|}{\omega(G-S)}}`，其中 `S\inC(G)`

    简单理解：`|S|` 是某个点割中包含的节点的个数，`\omega(G-S)` 是删除点割后出现的分支数，二者的比值越大，则说明删除了点割后对图的破坏性更小，图的坚韧度越高，反之亦然。