⚠ 转载请注明出处:作者:ZobinHuang,更新日期:Apr.30 2022
本作品由 ZobinHuang 采用 知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议 进行许可,在进行使用或分享前请查看权限要求。若发现侵权行为,会采取法律手段维护作者正当合法权益,谢谢配合。
目录
有特定需要的内容直接跳转到相关章节查看即可。
欧拉图及其性质
定义
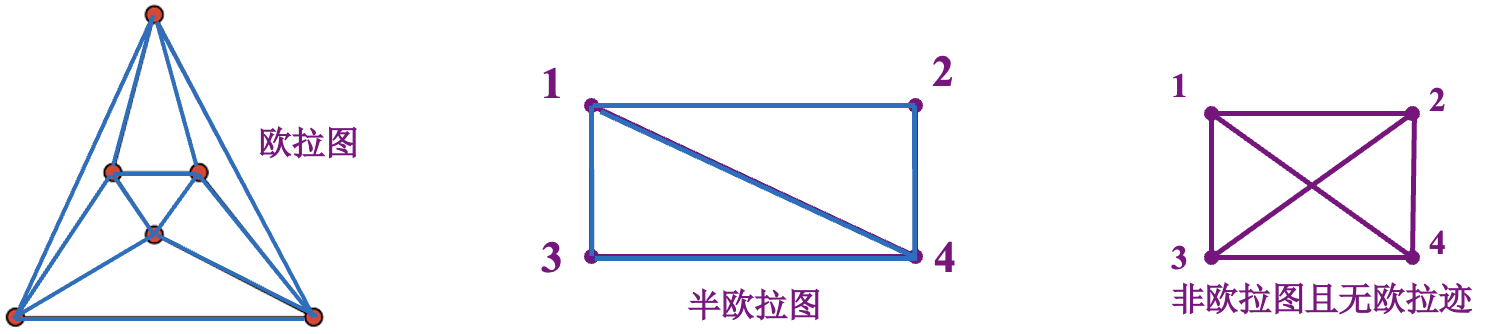
如果存在一条迹,起点和终点不同,并且经过一个图的所有边,则说这是一条
如果存在一条迹,起点和终点相同,并且经过一个图的所有边,则说这是一条
对连通图 `G` (p.s.
欧拉闭迹又称为
性质
下面给出关于欧拉图性质的定理
- `G` 是欧拉图
- `G` 的每个顶点的度均为偶数
- `G` 的边集能划分为边不交圈的并
证明:
首先证明 [1] `\rightarrow` [2]: 由 [1], 设 `C` 是欧拉图 `G` 的任一欧拉环游, `v` 是 `G` 中任意顶点, `v` 在环游中每出现一次, 意味在 `G` 中有两条不同边与 `v` 关联。所以, 在 `G` 中与 `v` 关联的边数为偶数,即 `v` 的度数为偶数, 由 `v` 的任意性,即证明 [2]。
然后证明 [2] `\rightarrow` [3]: 由于 `G` 是连通非平凡的且每个顶点度数为偶数 (`\delta \ge 2`), 所以 `G` 中至少存在圈 `C_1`, 从 `G` 中去掉 `C_1` 中的边, 得到 `G` 的生成子图 `G1`。
- 若 `G_1` 没有边,则 [3] 成立;
- 否则, `G_1` 的每个非平凡分支是度数为偶数的连通图 (i.e. 删完 `G_1` 后顶点度数的奇偶性不变),于是又可以抽取一个圈。反复这样抽取,`E(G)` 最终划分为若干圈
最后证明 [3] `\rightarrow` [1]: 设 `C_1` 是 `G` 的边划分中的唯一的圈。若 `G` 仅由此圈组成, 则 `G` 显然是欧拉图。否则, 由于 `G` 连通,所以,必然存在圈 `C_2`, 它和 `C_1` 有公共顶点。于是,`C_1 \cup C_2` 是一条含有 `C_1` 与 `C_2` 的边的欧拉闭迹,如此拼接下去,得到包含 `G` 的所有边的一条欧拉闭迹。即证 `G` 是欧拉图。
基于上面的推到,我们可以下面给出两个推论:
关于卡式乘积 (p.s. 卡式乘积定义见 Cartesian 积图),又如下结论:
证明:
由于做了卡式乘积,因此对于任意的 `u \in V(G)`,`v \in V(H)`,有:
所以,`G □ H` 每个顶点的度数均为偶数。下面我们只要证明 `G □ H` 是一个连通图,即可证明 `G □ H` 是一个欧拉图。
对于 `\forall (u_1,v_1)`, `(u_2,v_2) \in V(G □ H)`,由于 `G` 和 `H` 都是欧拉图,因此它们都是连通图。设最短的 `u_1,u_2` 路和最短的 `v_1,v_2` 路分别为: `u_1x_1x_2...x_ku_2` 和 `v_1y_1y_2...y_mv_2`。那么由 `G □ H` 的定义,在 `G □ H` 中就有路:
因此 `G □ H` 是一个连通图,加上它每一个顶点都是偶数,它就是一个欧拉图。
Fleury 算法
- 任意选择一个顶点 `v_0`,置初始迹 `w_0=v_0`;
-
假设迹 `w_i=v_0e_1v_1…e_iv_i` 已经选定, 那么按下述方法从 `E−{e_1, e_2, …, e_i}` 中选取边 `e_{i+1}`:
- `e_{i+1}` 与 `v_i` 相关联;
- 除非没有别的边可选择, 否则 `e_{i+1}` 不能是 `G_i=G−{e_1, e_2, …, e_i}` 的割边 (避割边);
- 当 (2) 不能执行时,算法停止.
下面给出一个基于 Fleury 算法证明的定理:
证明:
不失一般性,就图是连通图进行证明。
设图 `G` 的 `2k` 个奇度点分别是 `v_1`, `v_2`, `...`, `v_k`, `v_{k+1}`, `...`, `v_{2k}`。我们在 `v_i` 和 `v_{i+k}` 之间连新边 `e_i`,得到图 `G^{\star}` `(1 \le i < k)`。由于此时所有的奇数点都已经被消除,所以 `G^{\star}` 是欧拉图。因此,由 Fleury 算法可以得到欧拉环游 `C`。
对于得到的欧拉环游 `C`,在 `C` 中删去 `e_i` `(1 \le i \le k)`,即得到 `k` 条边不重的迹 `Q_i` `(1 \le i < k)`:
中国邮递员问题
问题定义是这样的: 一名邮递员从邮局出发派发邮件,要经过他所管辖区域的每一条街道最后返回邮局(每条街道可以经过不止一次),如何安排路线,才能使邮递员走过的总路程最短呢?
管梅谷给出的定理是:
- `G` 的每条边在 `W` 中最多重复一次 (i.e. 出现两次);
- 对于 `G` 的每个圈上的边来说,在 `W` 中重复的边的总权值不超过该圈非重复边总权值。
简单地进行理解,中国邮递员针对的图不一定是欧拉图,因此就有可能存在奇数度的点。在上面的条件中,(1) 出现重复边的目的是消除奇数度的点,而这样的操作需要一次就可以进行消除了,因此最多重复一次。下面我们进行证明。
证明: (只证明必要性)
首先,设 `G` 是连通非欧拉图,`u` 与 `v` 是 `G` 的两个奇度顶点,把连接 `u` 与 `v` 的路上的边改为 `2` 重边,则路中的点的度数奇偶性没有改变,仍然为偶数,但 `u` 与 `v` 的度数由奇数变成了偶数。如果对 `G` 中每对奇度点都如此处理,则最终得到的图为欧拉图。设该图为 `G_1`。
其次, 对 `G_1` 作修改:
如果在 `G_1` 中,边 `e` 重复数大于 `2`,则在 `G_1` 中删掉 `2` 条重复的 `e` 边后,所得之图仍然是包含 `G` 的欧拉图。在 `G_1` 中,对每组平行边都做这样的处理,最后得到一个重复边数最多为 `1` 的包含 `G` 的欧拉图 `G_2`。
这说明,若 `W` 是包含 `G` 的所有边的欧拉环游,则 `G` 中每条边至多在 `W` 里出现两次,这就证明了 (1)。
又设 `C` 是 `G2` 中
必要性证毕。
管梅谷并没有提出好的算法,因此基于上述定理及其证明,只能通过穷举的方法来从图中找出一个最优欧拉环游。下面我们来看一个例子:
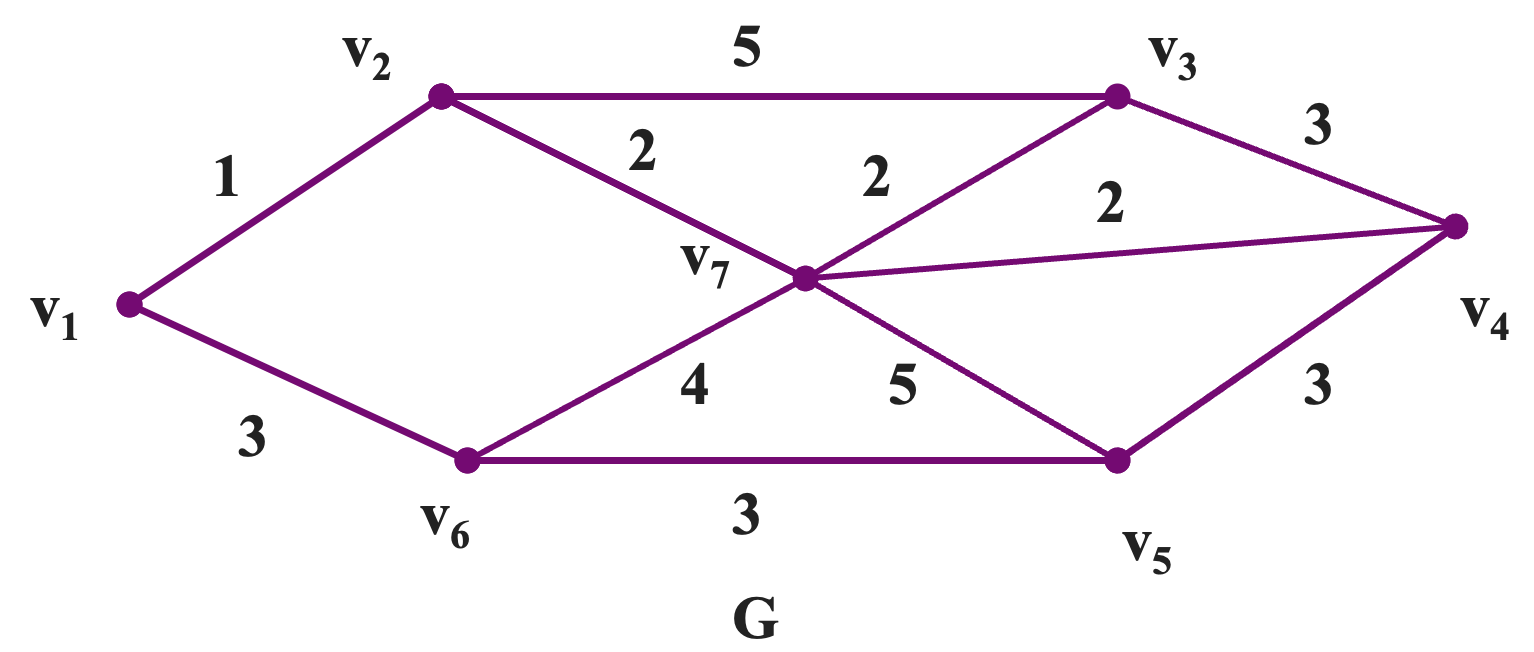
首先我们先将所有的奇数点补齐为偶数度的点:
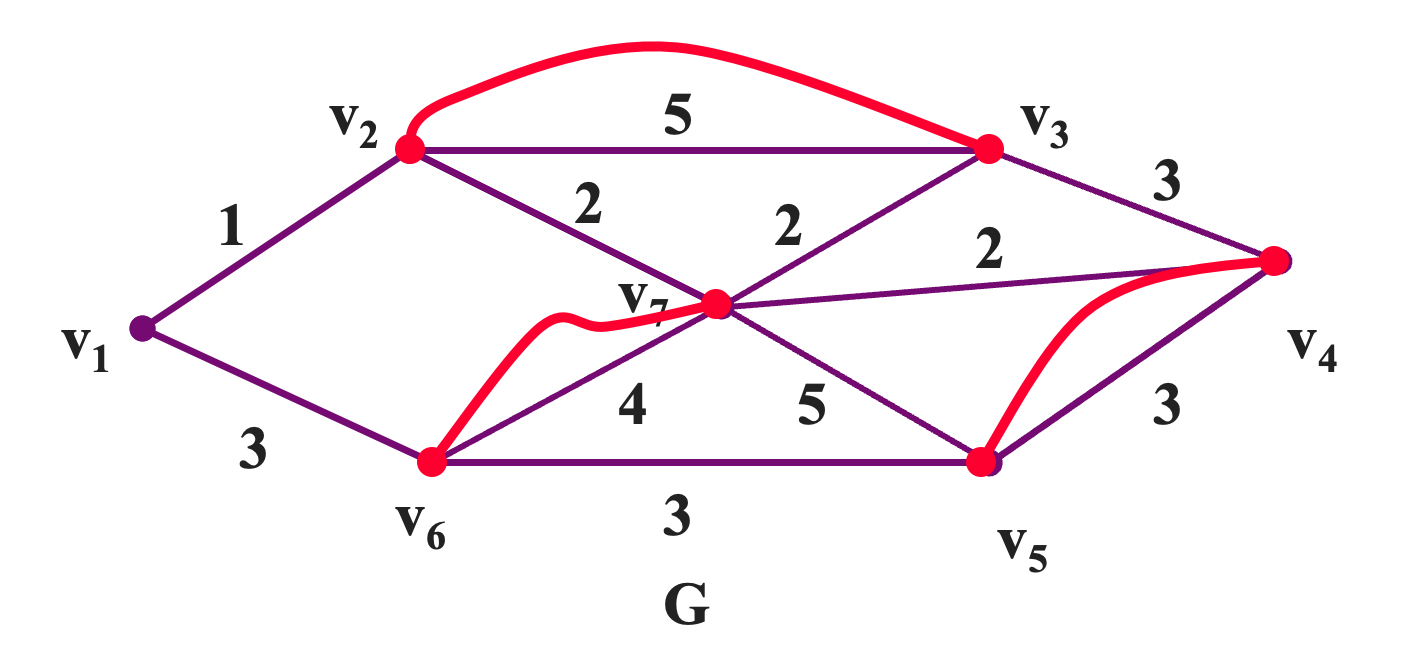
然后我们从图中观察各个圈,确认各个圈中的重边的权重和小于单边的权重和。如果不满足,则进行置换,如下所示:
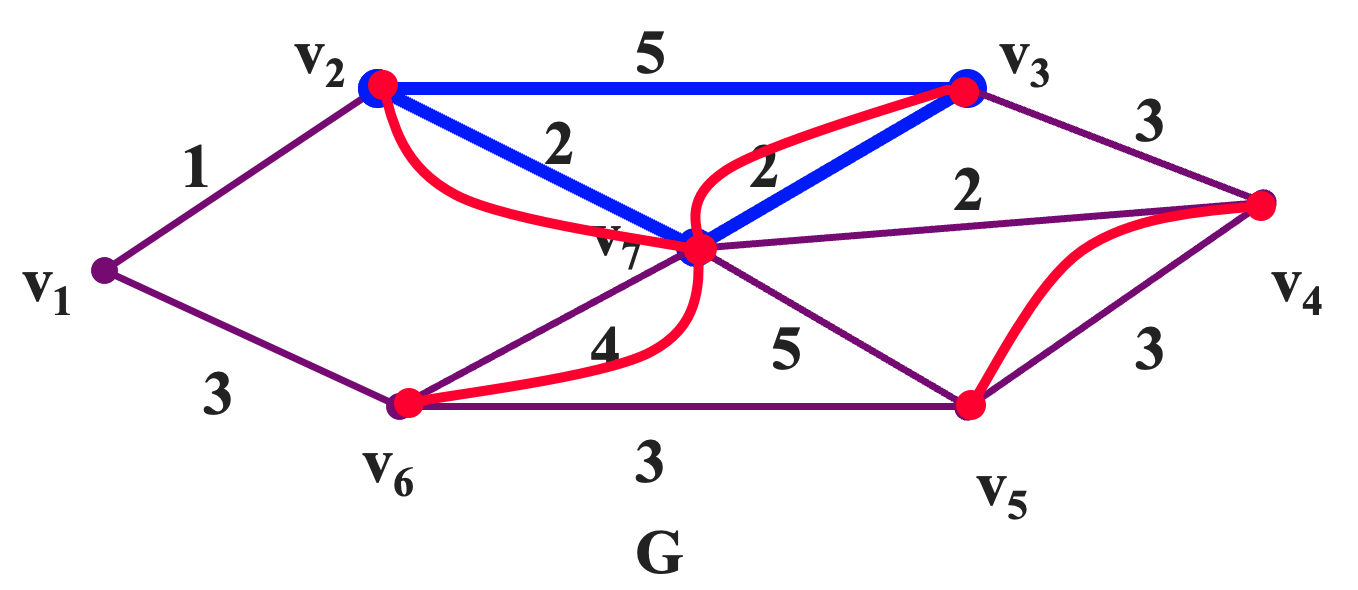
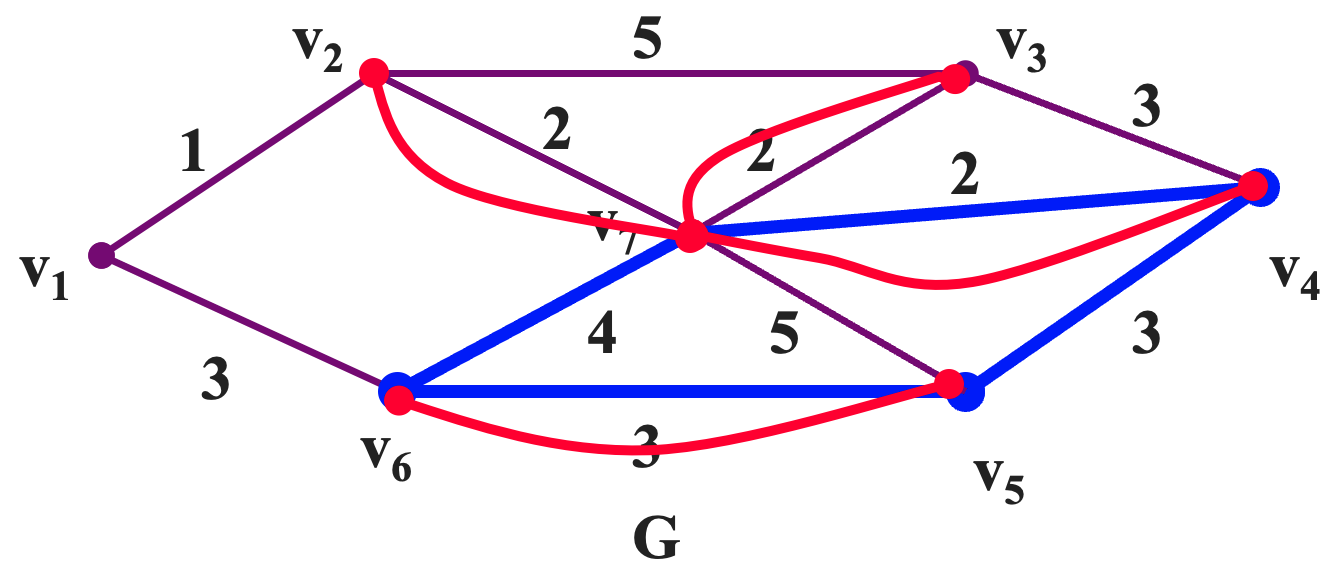
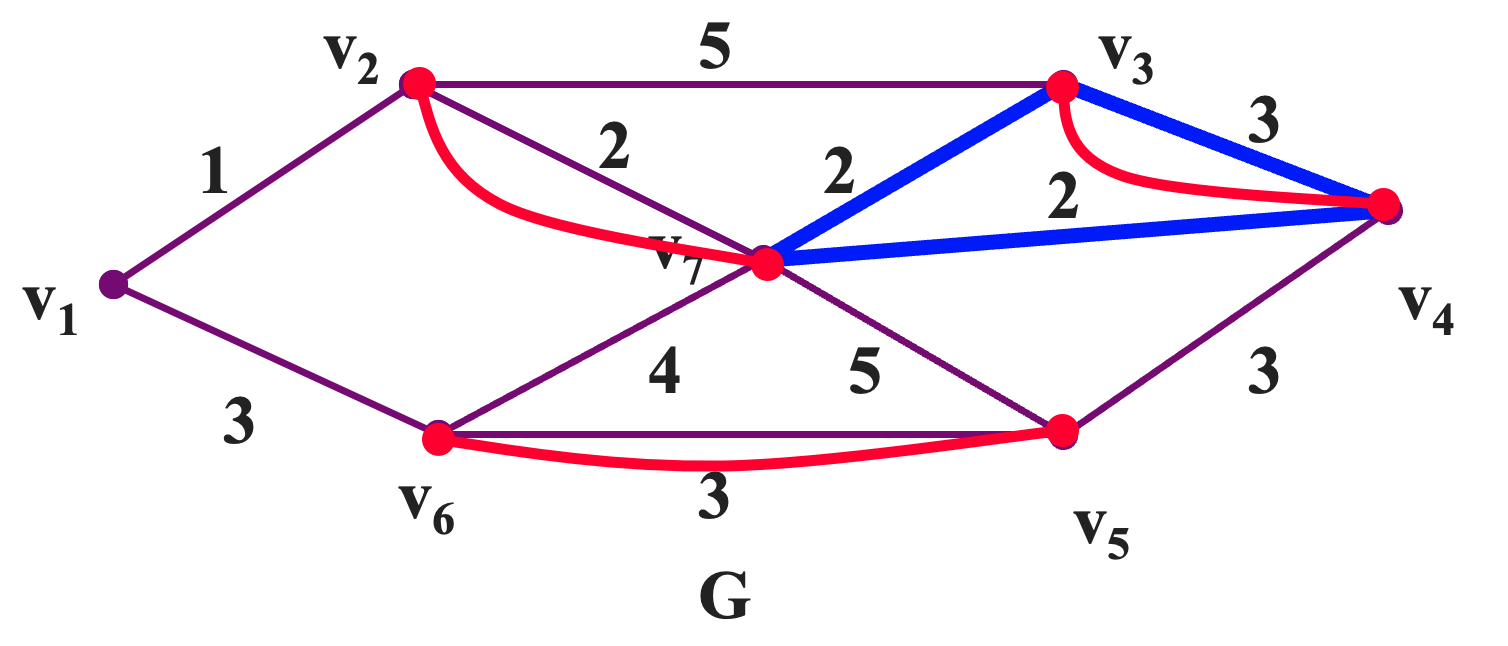
下面我们给出一个针对只有两个奇数点 `u` 和 `v` 的边赋权图 `G` 的求解最优欧拉环游的算法。
- 在 `u` 与 `v` 之间求出一条最短路 `P`;
- 在最短路 `P` 上,给每条边添加一条平行边得到 `G` 的欧拉图 `G^{\star}`;
- 在 `G` 的欧拉图 `G^{\star}` 中用 Fleury 算法求出来一条欧拉环游
下面我们证明算法求出的欧拉环游是最优的:
设 `u` 和 `v` 是两个奇度顶点,`G^{\star}` 是 `G` 上添加重复边的基础上得到的任意一个欧拉图。考虑 `G^{\star}[E^{\star}-E]`,显然它只有两个奇度点 `u` 与 `v` (i.e. 因为只保留了添加的边),当然它们必须在 `G^{\star}[E^{\star}-E]` 的同一个分支中,否则就存在其它的奇数点。因此,存在 `(u,v)` 路 `P^{\star}`。所以有:
