平面图的概念和性质

⚠ 转载请注明出处：作者：ZobinHuang，更新日期：Jan.30 2022

    本作品由 ZobinHuang 采用 知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议 进行许可，在进行使用或分享前请查看权限要求。若发现侵权行为，会采取法律手段维护作者正当合法权益，谢谢配合。

目录

有特定需要的内容直接跳转到相关章节查看即可。

正在加载目录...

平面图

概念

    如果能把图 $G$ 画在平面上，使得除顶点外，边与边之间没有交叉，称 $G$ 可以嵌入平面，或称 $G$ 是 可平面图 (Planar Graph)。可平面图 $G$ 的边不交叉的一种画法，称为 $G$ 的一种 平面嵌入，$G$ 的平面嵌入表示的图称为 平面图 (Plane Graph)。

    一个平面图 $G$ 把平面分成若干连通片，这些连通片称为 $G$ 的一个 面 (Face) 或 区域 (Region)，$G$ 的面组成的集合用 $\Phi$ 表示。面积有限的区域称为平面图 $G$ 的 内部面 (Inner Face)，否则称为 $G$ 的 外部面 (Outer Face)。

    如上图所示，$f_4$ 是一个外部面，$f_1$, $f_2$ 和 $f_3$ 是内部面。

    最后我们定义：对于一条连续的，自身不交的，起点和终点重合的(封闭的)曲线，其在平面图中的各条边构成一条 Jordan 曲线。

性质

    首先来看一个与 Jordan 曲线相关的结论:

平面上任意简单闭合的曲线 $J$ 把平面划分为 内部 (Interior $J$) 和 外部 (Exterior $J$)。

    1 表明连接内部点和外部点的任何连线都与 $J$ 相交。

    在 $G$ 中，顶点和边都与某个给定面关联的子图, 称为该面的 边界 (Boundary)。某面 $f$ 的边界中含有的边数 (割边计算 $2$ 次) 称为该面 $f$ 的 次数 (Degree)，记为 $deg(f)$。

    仍然以上图为例，$\deg(f_1)=1$, $\deg(f_2)=3$, $\deg(f_3)=6$, $\deg(f_4)=6$。

平面图的次数定理

    下面给出关于次数的定理:

设 $G=(n,m)$ 是平面图，则 $\sum_{f \in \Phi}deg(f) = 2m$

    证明: 对 $G$ 的任意一条边 $e$，如果 $e$ 是某个面内的割边，那么由面的次数定义，该边对 $G$ 的总次数贡献 $2$ 次。如果 $e$ 不是割边，那么它必然是两个面的公共边。因此, 由面的次数定义, 它也给总次数贡献2次. 于是有上述结论。

平面图的欧拉公式

    下面给出平面图的欧拉公式。:

设 $G=(n,m)$ 是连通平面图，$\phi$ 是 $G$ 的面数，则有 $n-m+\phi=2$

    证明: 对 $\phi$ 作归纳。

    当 $\phi=1$ 时，这个图只有一个面，也即只有外部面，是一个无圈的图，也即为树。有 $m=n-1$，故上述定理成立。

    设恒等式对所有小于 $\phi$ ($\phi>1$) 个面的图都成立。

    考虑面数为 $\phi$ 的情形，取 $G=(n,m)$ 的一条非割边 $e$，则 $G-e$ 打通了两个平面，也即 $G-e$ 是包含 $\phi-1$ 个面的平面图，由归纳假设得 $|V(G-e)|-|E(G-e)|+|\phi(G-e)|=2$。易知 $|V(G-e)|=n$, $|E(G-e)|=m-1$, $|\phi(G-e)|=\phi-1$，因此有 $n-m+\phi=2$ 成立。

    平面图的欧拉定理有如下推论:

设 $G$ 是具有个面 $k$ 个连通分支的平面图, 则 $n-m+\phi=k+1$

    证明: 对第 $i$ 个分支来说，设顶点数为 $n_i$，边数为 $m_i$，面数为 $\phi_i$，由欧拉公式可得: $n_i-m_i+\phi_i=2$，故有: $$\sum_{i=1}^k(n_i-m_i+\phi_i)=2k$$

    对于前两项，可得 $$\sum_{i=1}^{k}n_i=n, \sum_{i=1}^{k}m_i=m$$

    而对于最后一项，由于外部面被算了 $k$ 次，所以可知: $$\sum_{i=1}^{k}\phi_i = \phi + k -1$$

    综上可以得到: $$n-m+\phi=k+1$$

    下面给出一个推论:

设 $G$ 是具有 $n$ 个点 $m$ 条边ࣘ $\phi$ 个面的连通平面图，如果对 $G$ 的每个面 $f$，有 $deg(f) \ge l \ge 3$，则 $m \le \frac{l}{l-2}(n-2)$

    证明:

    一方面，由次数公式可得: $$2m=\sum_{f \in \Phi} \deg (f) \ge l \Phi$$

    因此可得: $\phi \le \frac{2m}{l}$。另一方面，由欧拉公式可得 $\Phi=2-n+m$，所以最终我们可以得到: $$\Phi = 2-n+m \le \frac{2m}{l}$$

    整理可得: $$m \le \frac{l}{l-2}(n-2)$$

    注意，5 的式子只是一个必要条件，而不是一个充分条件，也可平面图 $G$ 除了要满足 $m \le \frac{l}{l-2}(n-2)$ 条件只要，还需要有其它条件。

    5 实际上可以叙述为:

设 $G=(n,m)$ 是连通图，如果: $m > \frac{l}{l-2}(n-2)$，则 $G$ 是非可平面图

    若每个面 $f$ 都有 $\deg (f) \ge 3$ 或 $4$ 时，可以分别得到如下推论:

设 $G$ 是具有 $n$ $(n \ge 3)$ 个点 $m$ 条边ࣘ $\phi$ 个面的简单平面图，则 $m \le 3n-6$

设 $G$ 是具有 $n$ $(n \ge 3)$ 个点 $m$ 条边ࣘ $\phi$ 个面的简单平面二部图，则 $m \le 2n-4$

    同样地，上述两个推论也是必要条件。

    下面我们分别使用数值关系的方法，对两个图的非可平面性进行证明。

$K_5$ 不可平面

    证明:

    由于 $K_5$ 是简单图，$m=10$，$n=5$，则由 7 有 $3n-6=9$。由于 $|E(K_5)|=20>9$，因此 $K_5$ 是非可平面图。

$K_{3,3}$ 不可平面

    证明:

    首先注意到 $K_{3,3}$ 是二部图，不存在奇圈，因此每个面的次数至少是 $4$，也即 $\forall f \in \Phi, \deg (f) \ge 4$。由 5 可得，若 $K_{3,3}$ 是可平面的，它应该满足 $m \le \frac{l}{l-2}(n-2) = \frac{4}{2}(6-2) = 8$。然而 $m=9$，因此 $K_{3,3}$ 是不可平面的。

设 $G$ 是具有 $n$ 个点 $m$ 条边的连通平面图,若 $G$ 的每个面均由长度是 $l$ 的圈围成，则可得: $$m(l-2)=l(n-2)$$

    证明:

    由欧拉公式和次数定理分别可得: $$n-m+\Phi=2$$ $$\sum_{f \in \Phi} \deg (f) = 2m$$

    整理即可得结论式子。

设 $G$ 是具有 $n$ 个点 $m$ 条边的简单平面图，则 $\delta \le 5$

    证明:

    若不然，设 $\delta \ge 6$

    由握手定理可得: $$6n \le \sum_{v \in V(G)}d(v) = 2m$$

    也即: $$m > 3n-6$$

    由 7 可得，这与图 $G$ 是简单平面图矛盾，因此得证。

一个简单连通平面图是 $2$ 连通的，当且仅当它的每个面的边界是圈

    证明:

    首先证明必要性。设 $G$ 是 $2$ 连通的简单平面图，$G$ 没有自环。那么 $G$ 没有割边，也没有割点。所以，每个面的边界一定是一条闭迹 (i.e. 边不重复的首尾相同的途径)。设 $C$ 是图 $G$ 的某面的边界，我们证明它一定为圈。

    若不然，设 $C$ 是 $G$ 的某面的边界，但它不是圈。由于 $C$ 是一条闭迹且不是圈，也即 $C$ 虽然首尾顶点相同，但是途中经过了相同的顶点超过一次，所以在 $C$ 中存在子圈。设该子圈是 $W_1$。因为 $C$ 是某面的边界，所以 $W_1$ 和 $C$ 的关系可以表示为如下所示的形式:

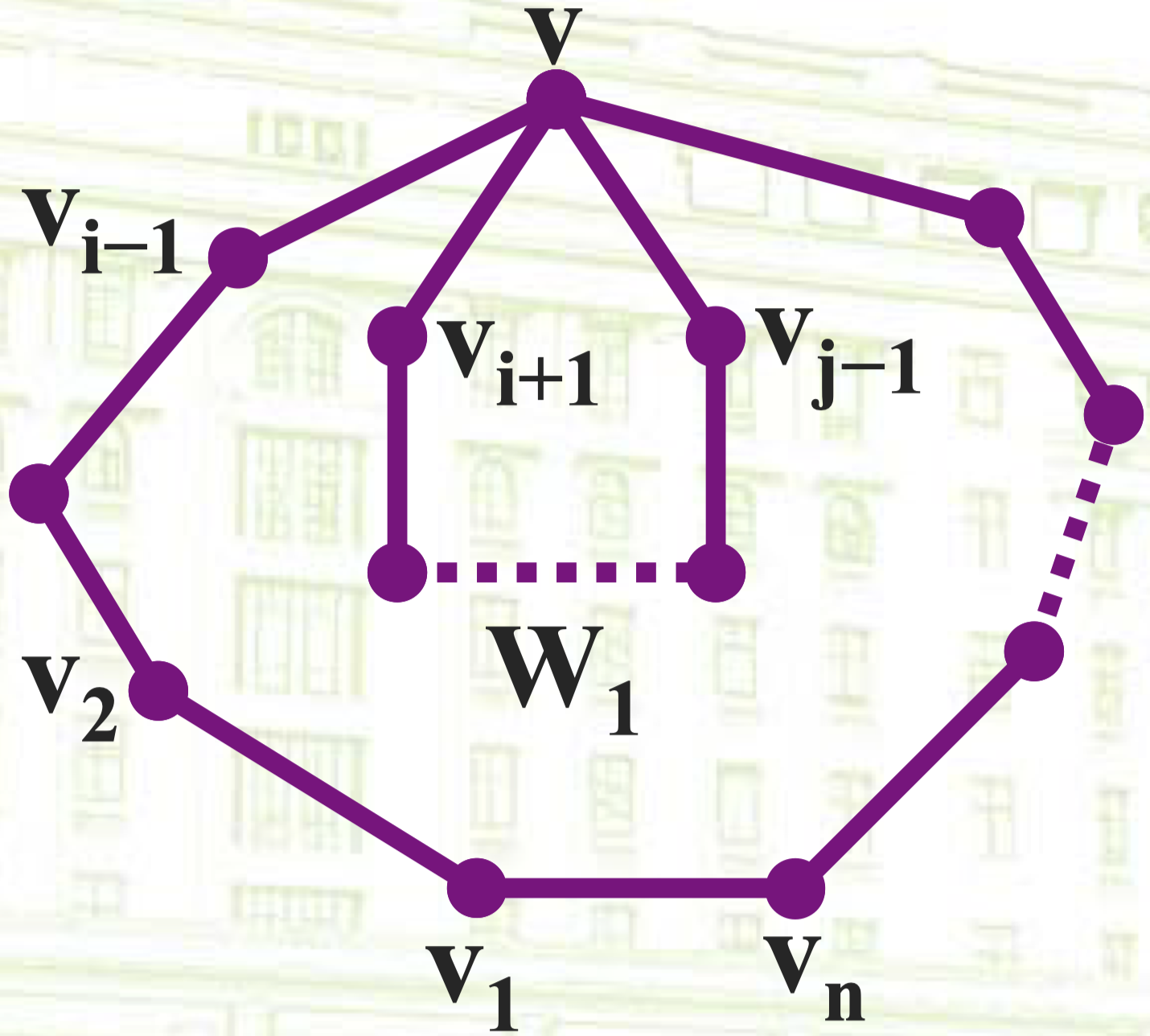
    可以发现图中的 $v$ 是一个割点，这与我们的假设冲突，因此 $C$ 一定是圈。

    下面证明充分性。设平面图 $G$ 的每个面的边界均为圈。此时删去 $G$ 中任意一个点不破坏 $G$ 的连通性，这表明 $G$ 是 $2$ 连通的。

    下面有一个推论:

若一个平面图是 $2$ 连通的，则它的每条边恰在两个面的边界上。

正多面体和富勒烯图

正多面体

    本节给出关于正多面体的相关性质。

存在且只存在 $5$ 种正多面体: 它们是正四、六、八、 十二、二十面体。

    证明:

    任取一个正ࣘ面体，其顶点数、棱数分别是 $n$ 和 $m$。对应的平面图是一个每个面次(度)数为 $l$，顶点度数为 $r$ 的简单平面正则图 $G$。

    由次数公式可得: $2m = \Phi l$，

    由握手定理可得: $2m = nr$。

    以上两式中，$l \ge 3$, $r \ge 3$。上述两市可以化简为： $$m = \frac{nr}{2}$$ $$\Phi = \frac{2m}{l} = \frac{nr}{l}$$

    代入欧拉公式 $n-m+\Phi = 2$ 可以得到： $$ n = 4l (2l-lr+2r)^{-1}$$

    基于上式可以提取出不等式 $2l-2r+2r>0$，也即 $2(l+r)>lr$。综上可以得到 \begin{cases} 2(l+r)>lr \\ l \ge 3 \\ r \ge 3 \end{cases}

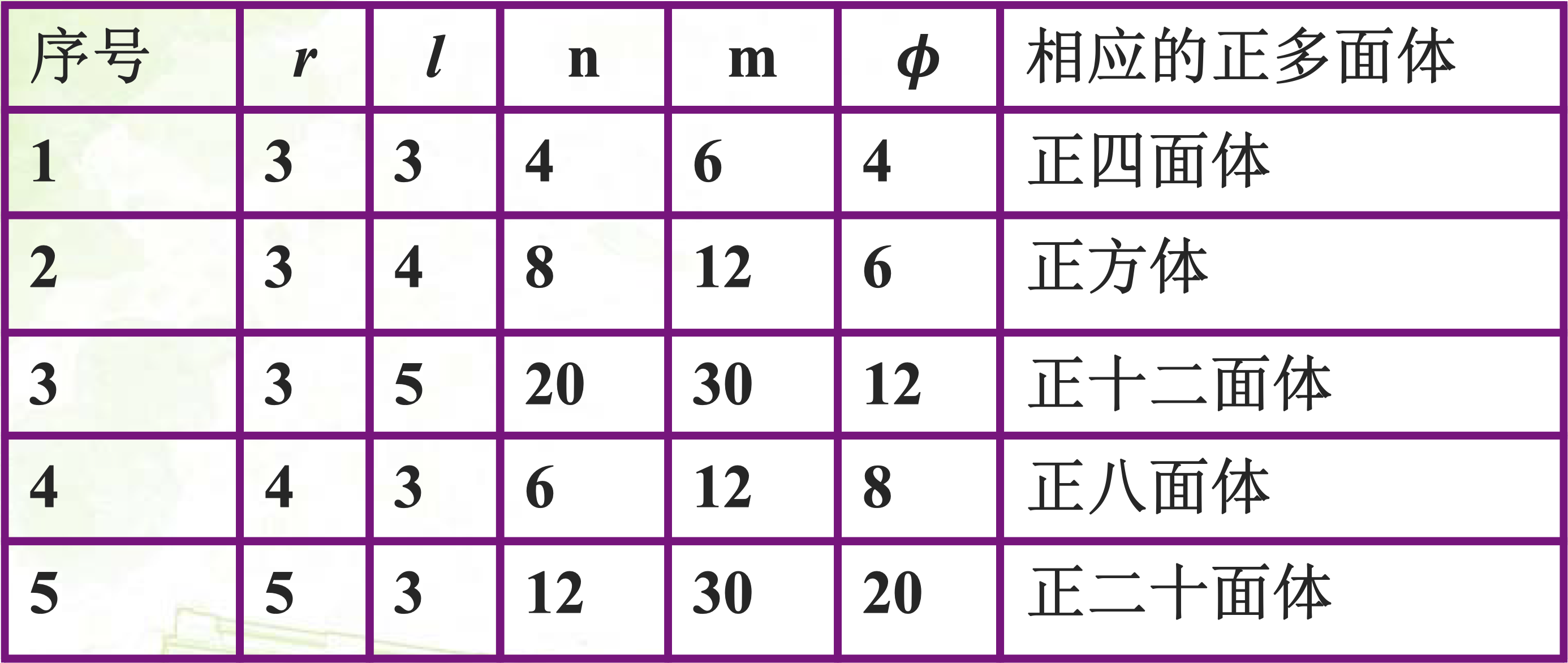
    满足上述不等式组的正整数解恰有 5 组：

富勒烯图

    富勒烯图 (Fullerene) 是所有面是五边形或者六边形的连通平面 $3$ 正则图。

富勒烯图恰好有 $12$ 个 $5$ 边形面。

    证明:

    令 $G$ 是一个富勒烯图。假设 $f_5$ 和 $f_6$ 分别表示 $G$ 的五边形面和六边形面的个数。

    由欧拉公式得 $n-m+\Phi=2$。

    由于 $G$ 是 $3$ 正则图，由握手定理可得 $3n=2m$。

    由面的次数公式可得 $5f_5 + 6f_6 = 2m$。

    另外我们可以得到 $\Phi = f_5 + f_6$。

    联立上述式子可以解得 $f_5=12$