图的路与连通性

⚠ 转载请注明出处：作者：ZobinHuang，更新日期：Mar.8 2022

    本作品由 ZobinHuang 采用 知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议 进行许可，在进行使用或分享前请查看权限要求。若发现侵权行为，会采取法律手段维护作者正当合法权益，谢谢配合。

目录

有特定需要的内容直接跳转到相关章节查看即可。

正在加载目录...

路与连通性

途径 (Walk)

    `G` 的一条 途径 (Walk) 是一个有限非空序列 `w=v_0e_1v_1e_2v_2…e_kv_k`，它的项交替地为顶点和边, 使得 `1 \le i \le k`, `e_i` 的端点是 `v_(i−1)` 和 `v_i`。

    途径中边数称为途径的 长度 (Length)，`v_0`, `v_k` 分别称为途径的 起点(initial vertex) 与 终点 (Terminal Vertex), 其余顶点称为途径的 内部点 (Internal Vertex)。

迹 (Trail)

    边不重复 的途径称为图 `G` 的一条 迹 (trail)。

路 (Path)

    顶点不重复 的途径称为图的一条 路，`n` 个点的路一般用 `P_n` 来表示。

    起点和终点重合的途径，迹和路分别称为图的 闭途径 (回路)，闭迹 和 圈。其中长度为 `k` 的圈称为 `k` 圈，`k` 为奇数的时候称为 奇圈，反之称为 偶圈，`n` 阶圈一般使用 `C_n` 表示。

距离 (Distance)

    图中点 `u` 与 `v` 的最短路的长度称为 `u` 与 `v` 之间的距离，记为 `d(u,v)`。如果 `u` 和 `v` 之间不存在路，则定义 `d(u,v)=\infty`。

连通性 (Connection)

    如果图中点 `u` 与 `v` 之间存在路，则说点 `u` 与 `v` 是 连通的 (Connected)，否则为 不连通的 (Disconnected)。

    规定一个顶点和它自身是连通的。

    如果图 `G` 中的任意两点是连通的，则说图 `G` 是一个 连通图 (Connected Graph)，否则为 非连通图 (Disconnected Graph)。

    图 `G` 中的每一个极大连通子图称为图 `G` 的 连通分支。可以这么定义连通分支：不存在 `G\'\' \supset G'`，使得 `G''` 仍能连通。图 `G` 的连通分支的个数，可以称为 `G` 的 分支数，记为 `\omega(G)`。

直径 (Diameter)

    定义连通图 `G` 的直径为: `d(G)=max{d(u,v)|u,v\inV(G)}`。如果 `G` 不连通，则定义 `d(G)=\infty`。

若 `\delta(G) \ge 2`，则图 `G` 中必然含有圈。

    上面的定理可以采用 最长路方法 来进行证明: 设 `P=v_1v_2…..v_{k-1}v_k` 是 `G` 中的一条最长路. 由于 `\delta \ge 2`, 所以 `v_k` 必然有相异于 `v_{k-1}` 的邻接顶点。又 `W` 是 `G` 中最长路，所以这样的邻接点必然是 `v_1`, `v_2`, …, `v_{k-2}` 中之一。设该点为 `v_m`, 则 `v_mv_{m+1}….v_kv_m` 为 `G` 圈。

连通图的性质

    我们给出连通图的两个性质。

若图 `G` 不连通，则其补图一定连通。

    证明过程很简单，分为两种情况: 对于 `\forall u,v \in V(\bar{G})`，

1. 若 `u`, `v` 属于 `G` 的同一分支，设 `w` 是与 `u`, `v` 处于不同分支中的点，则在 `\bar{G}` 中，`u` 与 `w`，`v` 与 `w` 分别相邻。于是 `u` 与 `v` 在 `\bar{G}` 中是连通的;
2. 若 `u`, `v` 属于 `G` 的不同分支，则`u` 与 `v` 在 `\bar{G}` 中必然是连通的

若 `G` 是简单图且 `\delta(G) \ge \frac{n-1}{2}`，则 `G` 是连通的。

    选择 `G` 的任意两点 `u` 和 `v`，这个定理的证明过程分为两种情况:

1. 若 `u` 和 `v` 相邻，则无需证明;
2. 若 `u` 和 `v` 不相邻，我们可以从这个图的特殊性入手，得到:
   `|N(u)| \ge \delta(G) \ge \frac{n-1}{2}`, `|N(v)| \ge \delta(G) \ge \frac{n-1}{2}`，故
   `|N(u)|+|N(v)| \ge 2 \cdot \delta(G) \ge n-1`，故
   `|N(u) \cap N(v)| = |N(u)| + |N(v)| - |N(u) \cup N(v)| \ge n-1 - (n-2) = 1`
   也即 `u` 和 `v` 至少有一个公共邻点

最短路算法

赋权图

    在图 `G` 的每条边上标上一个实数 `\omega(e)` 后，称 `G` 为 边赋权图。被标上的实数称为边的 权值 (Weight)。

    若 `H` 是赋权图 `G` 的一个子图, 称 `W(H)=\sum_{e\inE(H)}\omega(e)` 为子图H的权值。

    设 `G` 为边赋权图。`u` 与 `v` 是 `G` 中两点，在连接 `u` 与 `v` 的所有路中，路中各边权值之和最小的路，称为 `u` 与 `v` 间的 最短路 (Shortest Path)。

动态规划

    传统的 贪心算法 的思路是: 每个求解的步骤都是取局部的最优解。这样的算法在一些情况下无法达到全局最优，因为算法有可能因为在某一步选取了一个局部最优解而错过全局最优解。

    而 动态规划 的思路则是，为了求出问题 `f(n)`，我们可以对与求解 `f(n)` 相关的 `f(n)` 的子问题 `f(i)` `(i \< n)` 进行最优解求解，如此递归最终堆砌出 `f(n)` 的最优解。

Dijkstra 算法

    Dijkstra 算法 是一种在赋权图中求由点 `u_0` 到 `G` 中所有顶点的最短路的好算法。

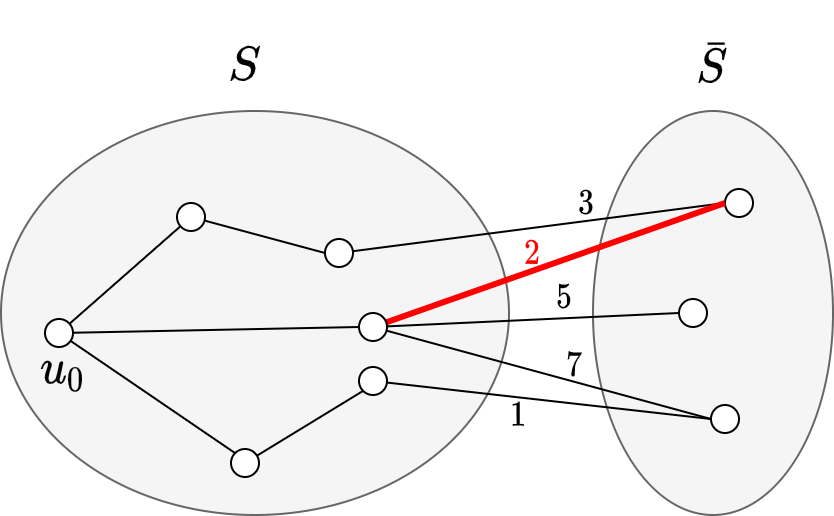
    Dijkstra 简单来说，就是把整个图分为两部分: 由未确定 `d(u_0, v')` 的顶点 `v'` 构成的子图 `\bar{S}`，以及由已经确定 `d(u_0, v)` 的顶点 `v` 构成的子图 `S`。算法的每次迭代，就是在子图 `S` 和 `\bar{S}` 之间的边界边上选取一条权重最小的边界边，然后把对应的位于 `\bar{S}` 的顶点加入到 `S` 中，形成新的 `S` 和 `\bar{S}`。算法初始化的时候，`S` 仅包含 `u_0` 一个顶点; 算法结束的时候，`\bar{S}` 将变为空集。