生成树的相关概念

⚠ 转载请注明出处：作者：ZobinHuang，更新日期：Mar.9 2022

    本作品由 ZobinHuang 采用 知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议 进行许可，在进行使用或分享前请查看权限要求。若发现侵权行为，会采取法律手段维护作者正当合法权益，谢谢配合。

目录

有特定需要的内容直接跳转到相关章节查看即可。

正在加载目录...

生成树的概念和性质

概念

    图 `G` 的一个生成子图 `T` 如果是树，称它为 `G` 的一棵 生成树 (Spanning Tree)。若 `T` 为森林，称它为 `G` 的一个 生成森林 (Spanning Forest)。

性质

    下面我们给出生成树的一些性质:

每个连通图至少包含一棵生成树。

    证明如下: 如果连通图 `G` 是树, 则其本身是一棵生成树。若连通图 `G` 中有圈 `C`，则去掉 `C` 中一条边后得到的图仍然是连通的。这样不断去掉 `G` 中圈，最后得到一个 `G` 的无圈连通子图 `T`，它为 `G` 的一棵生成树。这里的证明实际上给出了连通图 `G`的生成树的求法，该方法称为 (删边)破圈法。

    基于上述定理，我们可以有上述推论

若 `G` 是 `(n,m)` 的连通图, 则 `m \ge n-1`。

    证明过程其实很简单，其原因是因为树满足 `m(T)=n(T)-1`，故连通图有上述性质。

生成树的计数

    生成树的计数解决的是: 给定一个连通图，求出其可以导出的生成树的数量的问题。

Cayley 递推计数法

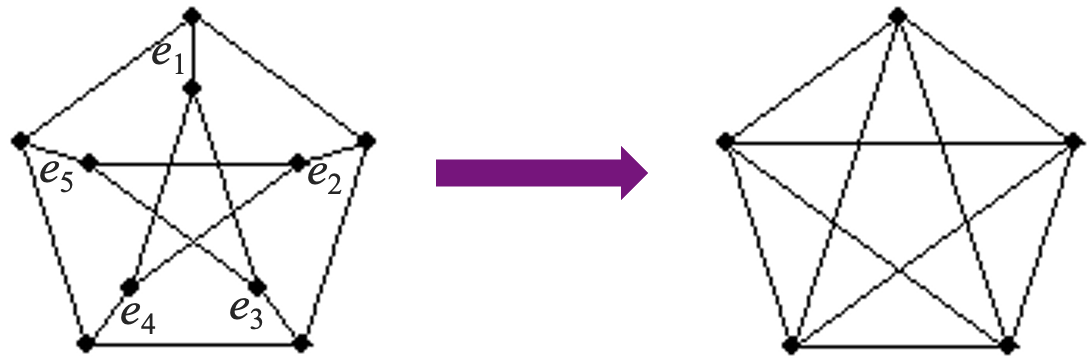
    图 `G` 的边 `e` 称为 被收缩 (Contraction)，是指删掉 `e` 后, 把 `e` 的两个端点 等同 (Identify)，如此得到的图记为 `G \cdot e`。具体如上图所示。

    用 `\tau(G)` 表示 `G` 的生成树棵数。

    Cayley 递推计数法是说:

设 `e` 是 `G` 的一条边(非自环)，则有: `\tau(G)=\tau(G-e)+\tau(G \cdot e)`

    我们给出证明: 考虑 `G` 中的一条边 `e`，`G` 的生成树中包含边 `e` 的棵数为 `\tau(G \cdot e)` (i.e. 与 `e` 关联的两个端点)，不包含边 `e` 的棵数为 `\tau(G - e)`，即证。(没有理解!!)

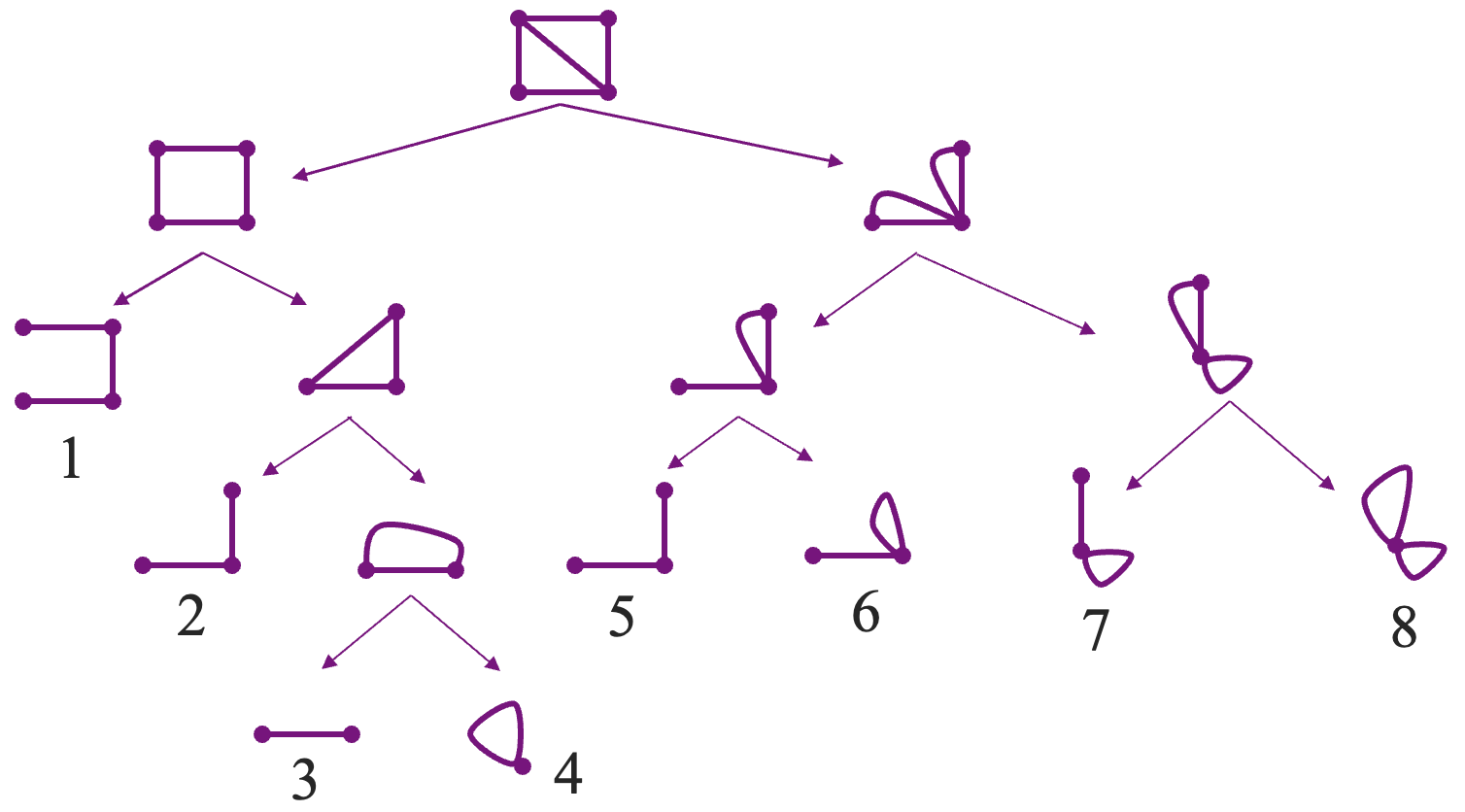
    Cayley 递推计数法的缺点是计算量非常大，并且不能具体指出每棵生成树。

矩阵树定理

    设 `G` 是顶点集合为 `V(G)={v1, v2, …, vn}` 的 无环图 (Loopless Graph), 设 `L=(l_{ij})` 是 `G` 的 Laplacian` 矩阵，其中:

`l_{ij} =` [1] `d(v_i)`, `i=j`; [2] `-a_{ij}`, `i \ne j`

则 `G` 的生成树棵数为 `L` 的任意一个元素 `l_{ij}` 的代数余子式的值。

回路系统简介

    设 `T` 是连通图 `G` 的一棵生成树，把属于 `G` 但不属于 `T` 的边称为 `G` 关于 `T` 的 弦 (Chord)，`T` 中的边称为 `G` 关于 `T` 的 树枝。

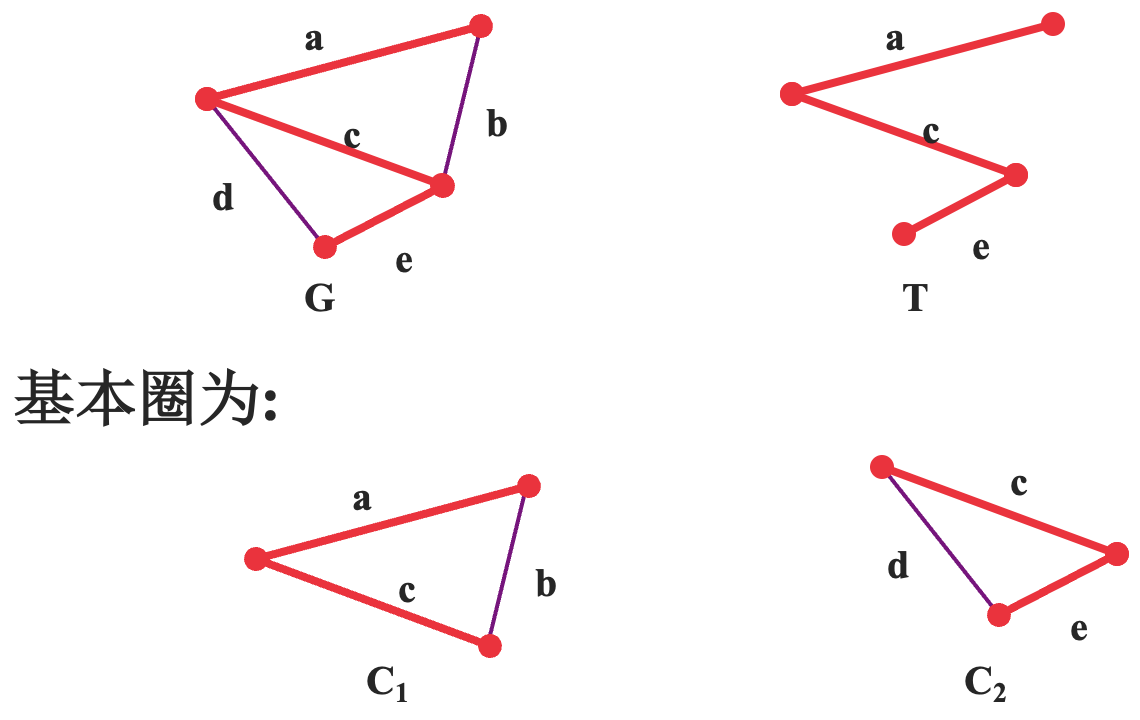
    设 `T` 是连通图 `G` 的一棵生成树，由 `G` 的对应于 `T` 的一条弦与 `T` 中的树枝构成的唯一圈 `C`，称为 `G` 关于 `T` 的一个 基本圈 (Fundamental Cycle)。若 `G` 是 `(n, m)` 连通图，把`G` 对应于 `T` 的 `m−n+1` 个基本圈称为 `G` 对应于 `T` 的 基本圈系统 (Fundamental Cycle System)，记为 `C_f`。

    基本圈系统拥有如下性质 (暂未理解含义和证明)。

设 `T` 是连通图 `G=(n, m)` 的一棵生成树，`C_1`, `C_2`, `…`, `C_{m−n+1}` 是 `G` 对应于 `T` 的基本圈系统。定义：`1 \cdot G_i = G_i`, `0 \cdot G_i = \emptyset`，`G_i` 是 `G` 的回路 (这里指每个点都是偶度的子图)。则 `G` 的回路组作成的集合对于该乘法和图的对称差运算构成数域 `F={0,1}` 上的 `m−n+1` 维向量空间.