Zobin

Lovin' Tech with Tea

在 Oneflow 中开发算子的基本流程

前言

    TODO

背景: GLU 及其变种的计算过程

前向计算过程

    参考 GLU Variants Improve Transformer glu_var_paper 这篇 Paper，GLU 及其变种的计算过程如下所示:

$\text{GLU}_{\text{Identity}}(X,W,V,B,C)=(XW+B)\otimes(XV+C)$
$\text{GLU}_{\text{sigmoid}}(X,W,V,B,C)=\sigma(XW+B)\otimes(XV+C)$
$\text{GLU}_{\text{relu}}(X,W,V,B,C)=\text{RELU}(XW+B)\otimes(XV+C)$
$\text{GLU}_{\text{gelu}}(X,W,V,B,C)=\text{GELU}(XW+B)\otimes(XV+C)$
$\text{GLU}_{\text{silu}}(X,W,V,B,C)=\text{SILU}(XW+B)\otimes(XV+C)$

    可以发现，上述变种的区别就在于计算式子中的激活函数不同，其余的计算过程基本一致: 给定一个输入张量 $X$，参数张量 $W$ 和 $V$，以及偏移张量 $B$ 和 $C$，首先进行 $(XW+B)$ 和 $(XV+C)$ 的线性运算 (p.s. 下文把前者的结果称为 gate，把后者的结果称为 hidden_state)；完成线性运算后，在 gate 上应用相应的激活函数 (p.s. 得到的结果下文称为 act_gate)；最终将 hidden_state 和 act_gate 上应用 Element-wise 的乘法，得到最终的结果。下面我们就这个计算式，对我们将要设计的算子的输入输出进行分析。

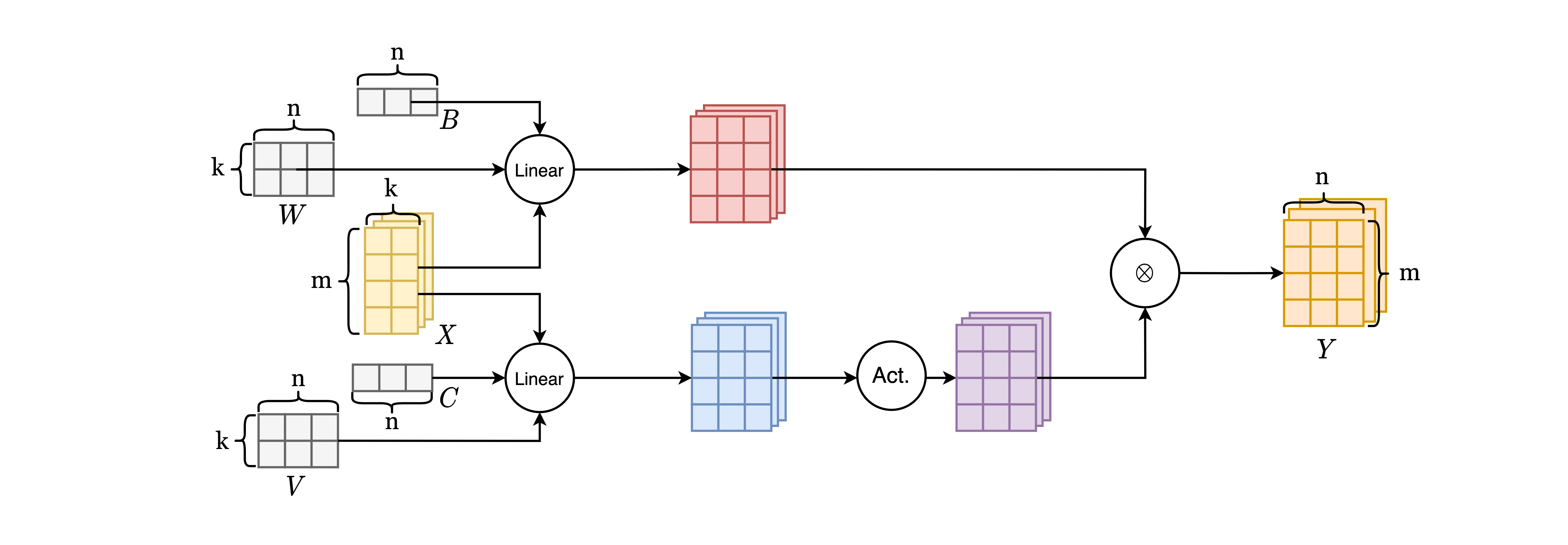
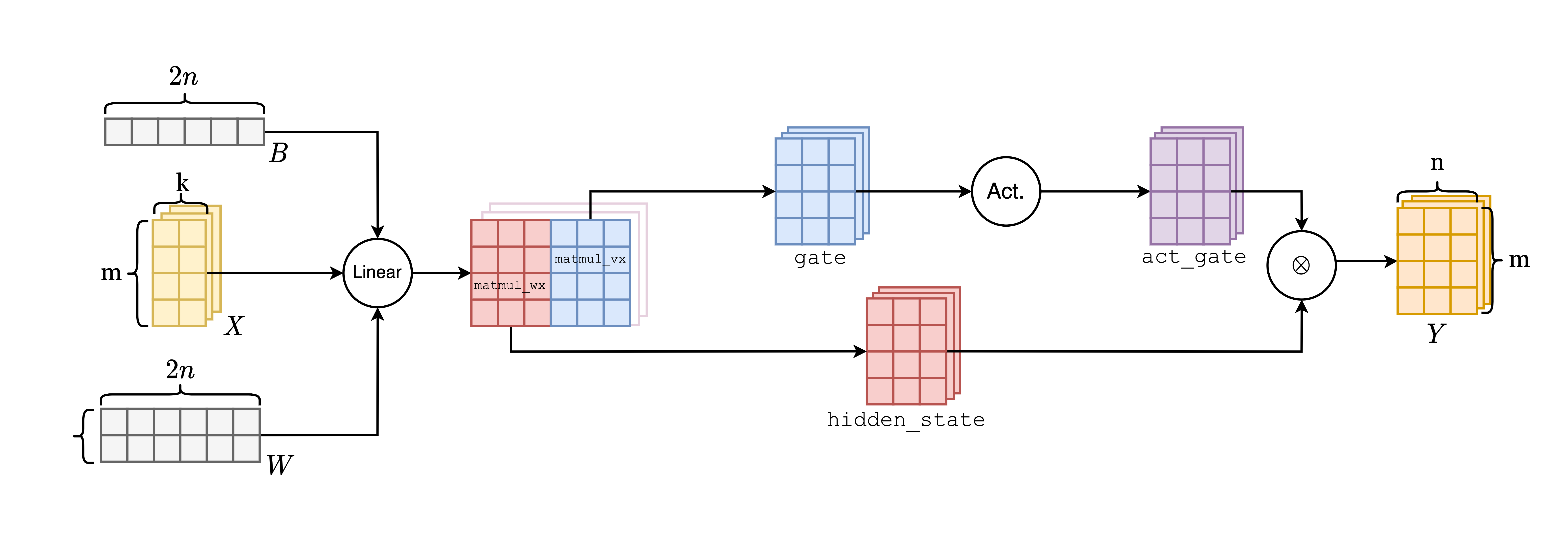
    上面描述的计算过程如 img_fused_glu_split 所示，用户提供形状为 $\underbrace{[..., m, k]}_{\text{可能不止两维}}$ 的输入张量 $X$，形状为 $[k, n]$ 的参数张量 $W$ 和 $V$ (p.s. 通常被转置为 $[n, k]$ 提供)，以及形状为 $[n]$ 的偏移张量 $B$ 和 $C$，GLU 输出一个形状为 $[..., m, n]$ 的张量。

    同时，我们也可以允许用户给定一个合并的参数张量和一个偏移张量，如 img_fused_glu 所示，用户仅提供形状为 $[m, k]$ 的输入张量 $X$，$[k, 2n]$ 的参数张量 $W$ 以及 $[2n]$ 的偏移张量 $B$，通过在算子内部进行 Chunk 操作，我们可以实现和上面一样的计算过程。这样一来，我们的算子就需要对输入的张量进行判断: 如果同时提供了 $X$, $W$, $V$, $B$ 和 $C$ 五个输入张量，则运行 img_fused_glu_split 所示的计算过程; 如果只提供了 $X$, $W$, 和 $B$ 三个张量，则运行 img_fused_glu 所示的计算过程。在下文中，我们把前者称为 Merged 实现，后者称为 Splited 实现。

Motivation: 为什么需要为 GLU 构造 Fused 实现?

性能之殇

Naive 实现

    采用最 Naive 的方法，我们可以在 Oneflow 中通过构造继承自 nn.Module 的类来实现 GLU 的计算过程，源码如下: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import os
import numpy as np
import oneflow as flow
import oneflow.nn as nn

class Glu(nn.Module):
  def __init__(self):
      super().__init__()

  def forward(
      self,
      x: flow.Tensor,             # 输入张量 x
      w: flow.Tensor,             # 参数张量 w
      b: flow.Tensor,             # 偏移张量 b
      v: flow.Tensor = None,      # 参数张量 v (optional)
      c: flow.Tensor = None,      # 偏移张量 c (optional)
      split_mode: bool = False,   # 指示是否是分离参数张量的输入
      activation: str = "none",   # 指示激活函数类型
  ) -> flow.Tensor:
      # matmul
      matmul_wx = flow._C.matmul(input=x, other=w, transpose_a=False, transpose_b=True)
      if split_mode:
          matmul_vx = flow._C.matmul(input=x, other=v, transpose_a=False, transpose_b=True)

      # add bias
      matmul_wx_b = flow._C.add(input=matmul_wx, other=b)
      if split_mode:
          matmul_vx_c = flow._C.add(input=matmul_vx, other=c)

      # chunk
      if split_mode:
          hidden_state = matmul_wx_b
          gate = matmul_vx_c
      else:
          hidden_state, gate = matmul_wx_b.chunk(2, dim=-1)

      # activation and element-wise product
      if activation == "none":
          return hidden_state * gate
      elif activation == "sigmoid":
          return hidden_state * flow.sigmoid(gate)
      elif activation == "relu":
          return hidden_state * flow.relu(gate)
      elif activation == "gelu":
          return hidden_state * flow.gelu(gate)
      elif activation == "fast_gelu":
          return hidden_state * flow._C.fast_gelu(gate)
      elif activation == "silu":
          return hidden_state * flow.silu(gate)

    我们就 Merged 实现分析一下上述程序运行一次前向传播所需要调用的底层 Kernels:

算子 底层调用的 Kernels
Matmul Line 21 调用的 flow._C.matmul 将最终调用 Primitive Matmul 完成运算 ofsrc_matmul_kernels_cpp，而后者则将调用 cuBLAS 的 API cublasGemmEx nvdoc_cublas_cublasgemmex 或 cublasGemmStridedBatchedEx nvdoc_cublas_cublasgemmstridedbatchedex 完成运算 ofsrc_broadcast_matmul_cpp
Add Line 26 调用的 flow._C.add 将最终调用 Primitive Add 完成运算 ofsrc_add_n_kernel_cpp，而后者则实现了相应的 CUDA Kernel AddGpu ofsrc_add_cu 完成运算
Chunk
Activation
Element-wise Multiplication

Naive 实现的性能测试

    对于上述实现，下面我们在不同的激活函数设置下，尝试向这段计算过程中打入不同规模的张量进行计算，并且获取计算过程的时延情况。完整的测试脚本如下所示: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
import os
import unittest
import time
import datetime
import numpy as np
from collections import OrderedDict

import oneflow as flow
import oneflow.nn as nn
import oneflow.unittest
from oneflow.test_utils.test_util import GenArgList

test_direction = "forward"

class Glu(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(
        self,
        x: flow.Tensor,
        w: flow.Tensor,
        b: flow.Tensor,
        v: flow.Tensor = None,
        c: flow.Tensor = None,
        split_mode: bool = False,
        activation: str = "none",
    ) -> flow.Tensor:
        # matmul
        matmul_wx = flow._C.matmul(
            input=x, other=w, transpose_a=False, transpose_b=True
        )
        if split_mode:
            matmul_vx = flow._C.matmul(
                input=x, other=v, transpose_a=False, transpose_b=True
            )

        # add bias
        matmul_wx_b = flow._C.add(input=matmul_wx, other=b)
        if split_mode:
            matmul_vx_c = flow._C.add(input=matmul_vx, other=c)

        # chunk
        if split_mode:
            hidden_state = matmul_wx_b
            gate = matmul_vx_c
        else:
            hidden_state, gate = matmul_wx_b.chunk(2, dim=-1)

        # activation and element-wise product
        if activation == "none":
            return hidden_state * gate
        elif activation == "sigmoid":
            return hidden_state * flow.sigmoid(gate)
        elif activation == "relu":
            return hidden_state * flow.relu(gate)
        elif activation == "gelu":
            return hidden_state * flow.gelu(gate)
        elif activation == "fast_gelu":
            return hidden_state * flow._C.fast_gelu(gate)
        elif activation == "silu":
            return hidden_state * flow.silu(gate)


def tensor_builder(params: dict, dtype=flow.float32, is_split_mode=True):
    # config test data
    m = params["m"]
    n = params["n"]
    k = params["k"]

    # generate random input
    x = np.random.randn(2, m, k) / 100
    y_nor = np.random.randn(2, m, n)
    if is_split_mode:
        w = np.random.randn(n, k) / 100  # transpose
        b = np.random.randn(n) / 100
        v = np.random.randn(n, k) / 100  # transpose
        c = np.random.randn(n) / 100
    else:
        w = np.random.randn(n * 2, k) / 100  # transpose
        b = np.random.randn(n * 2) / 100

    # transfer to gpu memory
    tensor_x = flow.FloatTensor(x).to(dtype=dtype, device="cuda")
    tensor_y_nor = flow.FloatTensor(y_nor).to(dtype=dtype, device="cuda")
    tensor_w = flow.FloatTensor(w).to(dtype=dtype, device="cuda").requires_grad_(True)
    tensor_b = flow.FloatTensor(b).to(dtype=dtype, device="cuda").requires_grad_(True)
    if is_split_mode:
        tensor_v = (
            flow.FloatTensor(v).to(dtype=dtype, device="cuda").requires_grad_(True)
        )
        tensor_c = (
            flow.FloatTensor(c).to(dtype=dtype, device="cuda").requires_grad_(True)
        )

    if is_split_mode:
        return tensor_x, tensor_w, tensor_b, tensor_v, tensor_c, tensor_y_nor
    else:
        return tensor_x, tensor_w, tensor_b, tensor_y_nor

def profile_naive_glu(test_case, params: dict, dtype=flow.float32):
    print(f"========== Start Testing ==========")
    print(f"impt: naive")
    print(f"direction: {test_direction}")
    print(f"weight tensor: merged")
    print(f'tensor shape: m={params["m"]}, n={params["n"]}, k={params["k"]}')
    print(f'activation: {params["act"]}')
    print(f"dtype: {dtype}")

    flow_module = Glu()
    x, w, b, y_nor = tensor_builder(params=params, dtype=dtype, is_split_mode=False)

    # forward
    if test_direction == "forward":
        y = flow_module.forward(x=x, w=w, b=b, split_mode=False, activation=params["act"])

    # backward
    if test_direction == "backward":
        y.sum().backward()

    print(f"============== PASSED =============")
    print("\n")

def profile_fused_glu(test_case, params: dict, dtype=flow.float32):
    print(f"========== Start Testing ==========")
    print(f"impt: fused")
    print(f"direction: {test_direction}")
    print(f"weight tensor: merged")
    print(f'tensor shape: m={params["m"]}, n={params["n"]}, k={params["k"]}')
    print(f'activation: {params["act"]}')
    print(f"dtype: {dtype}")

    x, w, b, y_nor = tensor_builder(params=params, dtype=dtype, is_split_mode=False)

    # forward
    if test_direction == "forward":
        fused_y = flow._C.fused_glu(x=x, w=w, b=b, v=None, c=None, activation=params["act"])

    # backward
    if test_direction == "backward":
        fused_y.sum().backward()

    print(f"============== PASSED =============")
    print("\n")

@flow.unittest.skip_unless_1n1d()
@unittest.skipIf(os.getenv("ONEFLOW_TEST_CPU_ONLY"), "only test gpu cases")
class TestFusedGlu(flow.unittest.TestCase):
    def test_gather(test_case):
        arg_dict = OrderedDict()
        # set up test functions
        arg_dict["test_fun"] = [
            profile_naive_glu,
            profile_fused_glu,
        ]

        # set up env valuable if necessary
        if not test_dualgemm_impt:
            os.environ["ONEFLOW_KERNEL_GLU_ENABLE_DUAL_GEMM_IMPL"] = "false"
        else:
            os.environ["ONEFLOW_KERNEL_GLU_ENABLE_DUAL_GEMM_IMPL"] = "true"

        # set up profiling functions
        if not test_dualgemm_impt:
            arg_dict["params"] = [
                # m=256, k=1280, n=5120
                {"m": 256, "k": 1280, "n": 5120, "act": "none"},
                {"m": 256, "k": 1280, "n": 5120, "act": "sigmoid"},
                {"m": 256, "k": 1280, "n": 5120, "act": "relu"},
                {"m": 256, "k": 1280, "n": 5120, "act": "gelu"},
                {"m": 256, "k": 1280, "n": 5120, "act": "fast_gelu"},
                {"m": 256, "k": 1280, "n": 5120, "act": "silu"},
                # m=1024, k=640, n=2560
                {"m": 1024, "k": 640, "n": 2560, "act": "none"},
                {"m": 1024, "k": 640, "n": 2560, "act": "sigmoid"},
                {"m": 1024, "k": 640, "n": 2560, "act": "relu"},
                {"m": 1024, "k": 640, "n": 2560, "act": "gelu"},
                {"m": 1024, "k": 640, "n": 2560, "act": "fast_gelu"},
                {"m": 1024, "k": 640, "n": 2560, "act": "silu"},
                # m=4096, k=320, n=1280
                {"m": 4096, "k": 320, "n": 1280, "act": "none"},
                {"m": 4096, "k": 320, "n": 1280, "act": "sigmoid"},
                {"m": 4096, "k": 320, "n": 1280, "act": "relu"},
                {"m": 4096, "k": 320, "n": 1280, "act": "gelu"},
                {"m": 4096, "k": 320, "n": 1280, "act": "fast_gelu"},
                {"m": 4096, "k": 320, "n": 1280, "act": "silu"},
                # m=2560, k=12800, n=51200
                {"m": 2560, "k": 1280, "n": 5120, "act": "none"},
                {"m": 2560, "k": 1280, "n": 5120, "act": "sigmoid"},
                {"m": 2560, "k": 1280, "n": 5120, "act": "relu"},
                {"m": 2560, "k": 1280, "n": 5120, "act": "gelu"},
                {"m": 2560, "k": 1280, "n": 5120, "act": "fast_gelu"},
                {"m": 2560, "k": 1280, "n": 5120, "act": "silu"},
            ]
        else:
            arg_dict["params"] = [
                # m=256, k=1280, n=5120
                {"m": 256, "k": 1280, "n": 5120, "act": "fast_gelu"},
                # m=1024, k=640, n=2560
                {"m": 1024, "k": 640, "n": 2560, "act": "fast_gelu"},
                # m=4096, k=320, n=1280
                {"m": 4096, "k": 320, "n": 1280, "act": "fast_gelu"},
                # m=2560, k=12800, n=51200
                {"m": 2560, "k": 1280, "n": 5120, "act": "fast_gelu"},
            ]

        if not test_dualgemm_impt:
            arg_dict["dtype"] = [flow.float16, flow.float32]
        else:
            arg_dict["dtype"] = [flow.float16]

        for arg in GenArgList(arg_dict):
            arg[0](test_case, *arg[1:])


if __name__ == "__main__":
    unittest.main()

    以 Sigmoid 为激活函数为例，当数据类型为 Half (2 Bytes) 和 Float (4 Bytes) 时，在不同张量形状输入下，将上面的测试脚本按照所执行的 Kernels 进行性能分解，如 naive_impt_performance_sigmoid_half 和 naive_impt_performance_sigmoid_float 所示:

    另外，当设置激活函数为其它形式时，测试结果收录在如下附录中:

激活函数 - Identity

激活函数 - Relu

激活函数 - Gelu

激活函数 - Fast Gelu

激活函数 - Silu

GLU 计算过程的 Kernel 理论运行时间

    TODO: 粗略地对这个计算过程的理论最优执行时间进行估算

    TODO: 计算各个张量形状下，开发 Fused Kernel 的收益比

    由于 Oneflow 的执行是异步的，也就是说 Python 脚本构建出的逻辑计算图的各个 Op 实际上在 Oneflow 的 Runtime 中的执行是异步执行的，因此我们并不能直接在 Python 脚本中对 Duration 进行测试，上述的结果是首先使用 ncu 工具对这段计算过程中调用的各个 Kernels 的 Duration 进行记录，然后将这些 Kernels 的执行时间进行相加得到的。下面我们简单阐述一下这个过程:

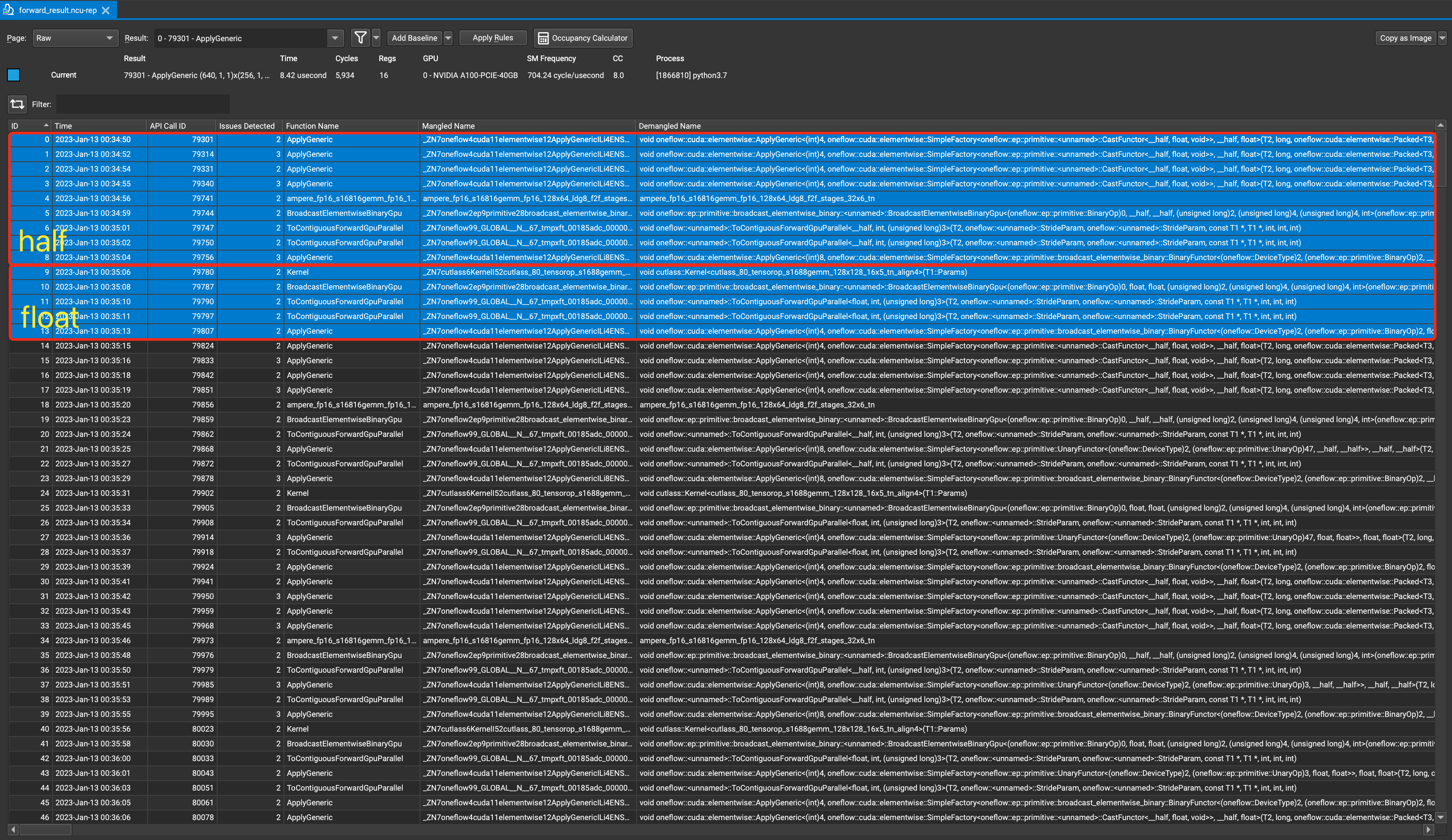
    结合上面给出的测试脚本，我们可以尝试将测试过程对应上在 Nsight Compute 中的相应记录结果。这里以前向传播的测试为例进行说明，如 img_forward_identity_ncu 所示，当我们设置 ① 激活函数为 Identity; ② 数据类型为 half/float; ③ 张量形状为 m=256, n=1280, k=5120 时，我们可以在图中的选中部分观察到对应调用的 Kernels。如果读者对 Oneflow 中相关算子的具体实现不是很熟悉，这里识别的技巧是:

  • Kernel 0~3 用于实际上是调用了 CastFunctor，其工作是将 half 类型的张量转换为 float 类型的张量，因此可以判断出这是针对 half 数据类型计算的开端;
  • Kernel 4~8 和 Kernel 9~13 实际上拥有类似的 Pattern，因此可以粗略判断出这两部分分别是 half 和 float 的计算过程;

    而实际上，这些 Kernels 的功能分析如下:

  • :

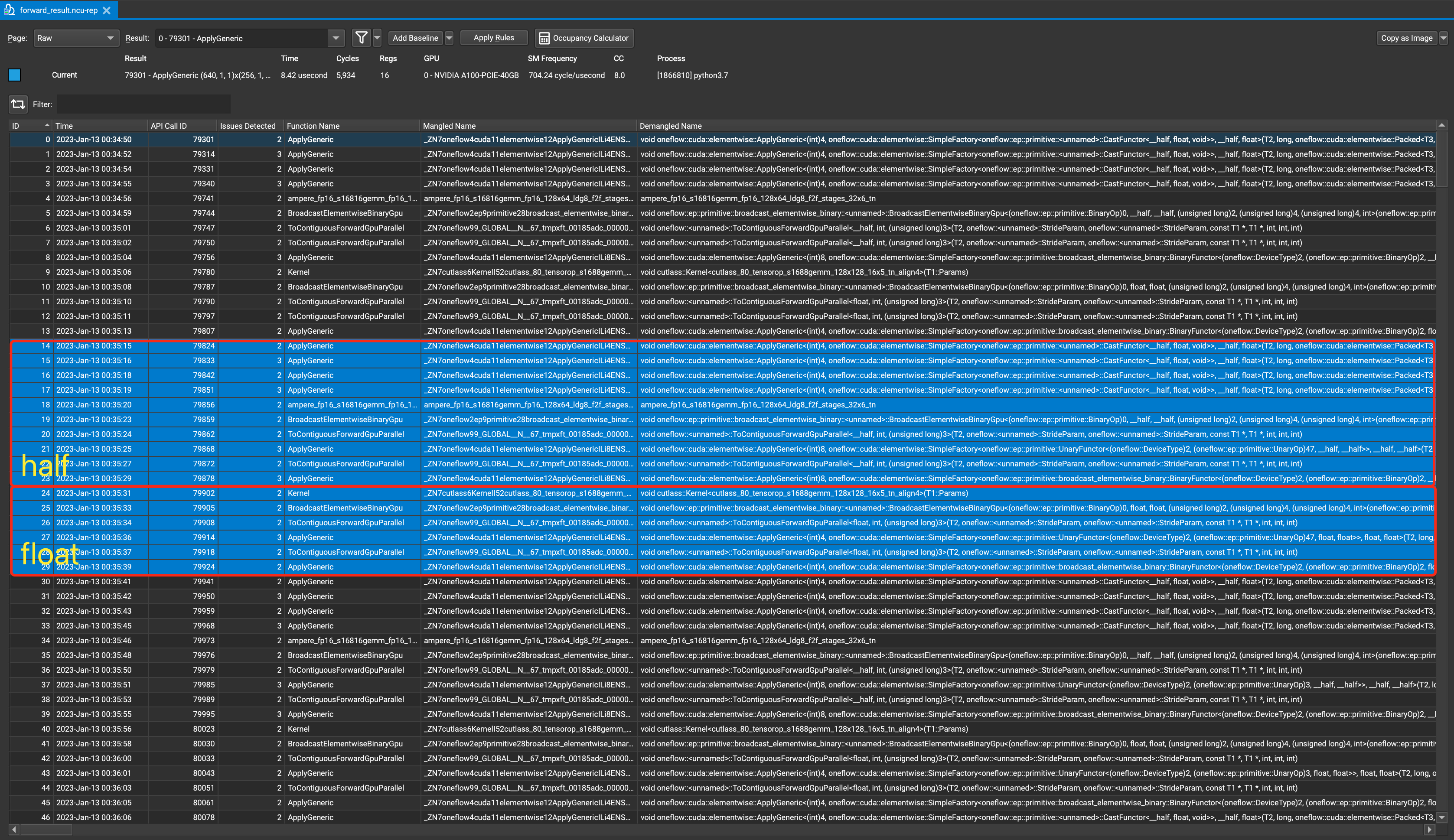
    同理，我们可以紧接着观察当我们设置 ① 激活函数为 Sigmoid; ② 数据类型为 half/float; ③ 张量形状为 m=256, n=1280, k=5120 时计算过程调用的 Kernels。我们可以发现大部分流程与上面激活函数为 Identity 时基本一致，不同的是 Kernel 21 和 27，它们实际上调用的是 Sigmoid 激活函数对应的 UnaryFunctor，我们在上面没有观察到对 UnaryFunctor 的调用是因为 Identity 实际上什么也没算，因此也无需调用任何 UnaryFunctor 来进行计算。

算子设计目标

    naive_impt_performance

定义 Operator