数据结构：图

⚠ 转载请注明出处：作者：ZobinHuang，更新日期：Mar.8 2021

本作品由 ZobinHuang 采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可，在进行使用或分享前请查看权限要求。若发现侵权行为，会采取法律手段维护作者正当合法权益，谢谢配合。

1. 与图有关的基本术语

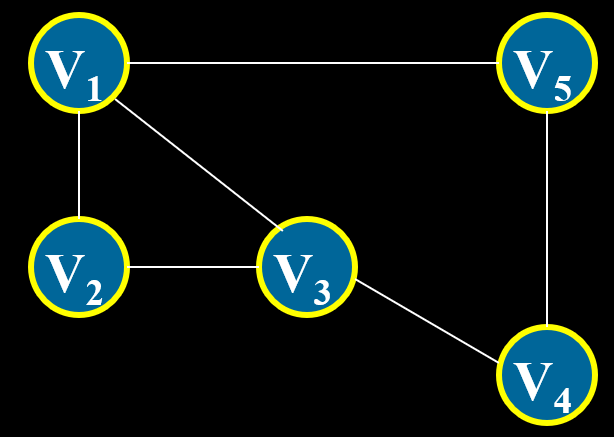
(1) 图：由 非空的顶点有限集 和 边的有限集 组成，记为 `G(V,E)` (V: Vertex, E: Edge)。相比于树，图对结点的前驱和后继结点个数不作限制。

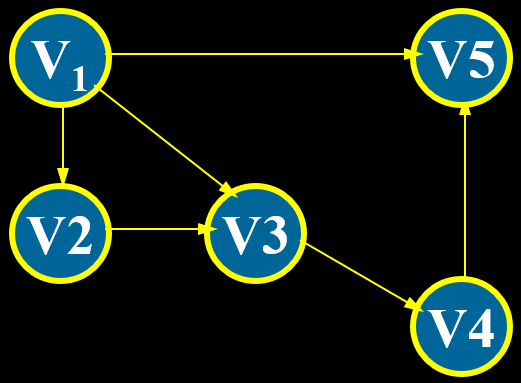
(2) 有向图：图中每条边都有方向，有向边又称弧。有向边以 `\langleV_i, V_j\rangle` （尖括号）表示，其中 `V_i` 是弧头，`V_j` 是狐尾，有向边 `\langleV_j, V_i\rangle` 和 `\langleV_i, V_j\rangle` 并不是同一条边。

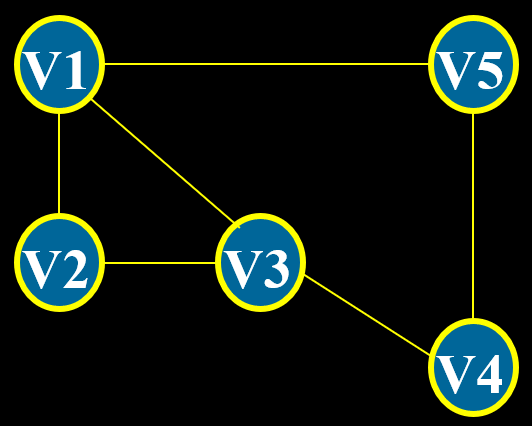
(3) 无向图：图中每条边都不设方向。无向边也以 `(V_i, V_j)` （圆括号）表示，且无向边 `(V_j, V_i)` 和 `(V_i, V_j)` 是同一条边。

(4) 邻接：若 `(V_i, V_j) \inE`，则 `V_i` 和 `V_j` 互为邻接关系。若 `\langleV_i, V_j\rangle \inE`，则 `V_j` 是 `V_i` 的邻接结点。

    (5) 顶点的度：
        对于有向图来说，顶点的出度即以该顶点为弧尾的弧的数目，顶点的入度即以该顶点为弧头的弧的数目，顶点的度 = 顶点的入度 + 顶点的入度。
        对于无向图来说，顶点的度即以该顶点为一个端点的边的条数。

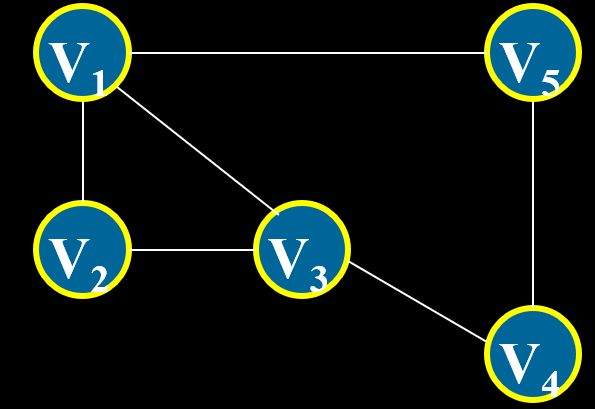
(6) 路径：从一个顶点到另一个顶点所经历的顶点序列。

(7) 环：第一个顶点与最后一个顶点相同的路径，例如上图所示的路径：`\underbrace{V_1 \rightarrow V_2 \rightarrow V_3 \rightarrow V_4 \rightarrow V_5 \rightarrow V_1}_{首尾相同}`

(8) 回路：序列中不出现重复的路径称为简单路径，有重复的路径称为回路，例如上图所示的回路：`\underbrace{V_1 \rightarrow V_2 \rightarrow V_1}_{出现重复} \rightarrow V_3`

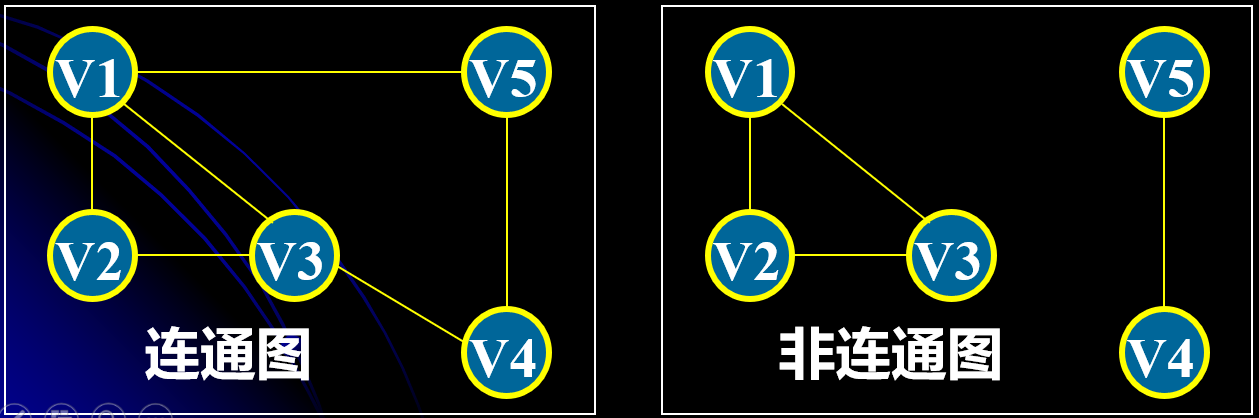
    (9) 连通图和非连通图：
        连通：若X和Y之间存在路径，则称X和Y之间是连通的。
        连通图：任意两个顶点都连通的图称为连通图，即没有孤立顶点。非连通图反之。
        连通分量：指无向图中极大连通子图的数目，即有多少个连通子图。如上图所示，左边的连通图有一个连通分量（任何连通图的连通分量只有一个），右边的非连通图有两个连通分量。

2. 图的存储

2.1 邻接矩阵

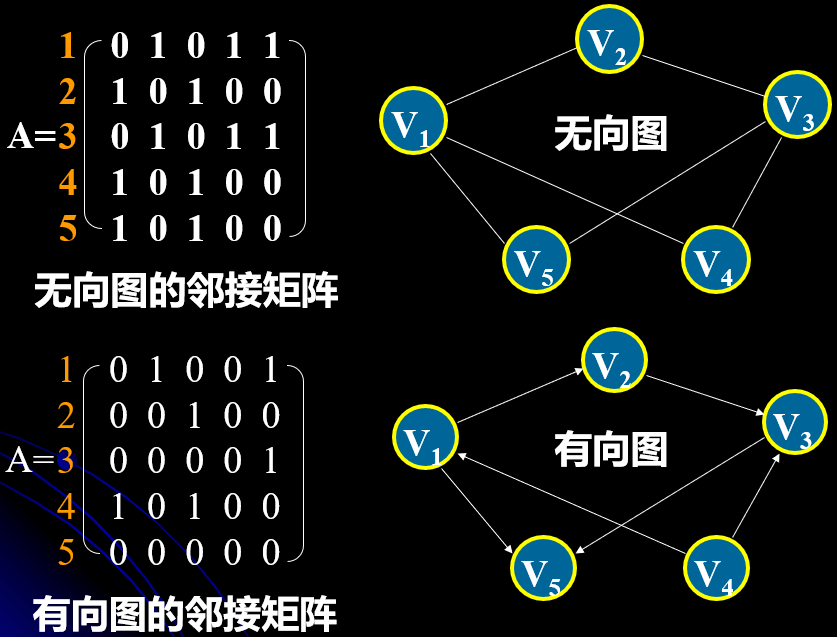
    若采用邻接矩阵存储图，则我们首先 ①先给顶点编号，然后 ②建立邻接（关系）矩阵 以呈现点与点之间的邻接关系。在邻接矩阵中，`a_(ij)` 的值表示i号顶点和j号顶点之间有无邻接关系，1即有，0即无，如上图所示。
    对于有向图来说，若 `a_(ij)` 为1，则表示存在从 `a_i` 出发到达 `a_j` 的一条弧。有向图顶点的出度为该行的元素之和，有向图顶点的入度为该列的元素之和。
    对于无向图来说，我们不难发现其邻接矩阵是一个对称矩阵，且无向图顶点的度是该行的元素之和。
    一般来说，如果 `N(边)` << `N^2(顶点)`，我们将这样的邻接矩阵成为稀疏矩阵。
    邻接矩阵实现起来十分简单，使用一个二维数组即可构造。基于邻接矩阵的图构造方法如下所示。

#define MAXNUM 100; /*图中顶点的最大个数*/
typedef struct graph{
  vertex node[MAXNUM];  /*一维数组，表示顶点的集合*/
  int arcs[MAXNUM][MAXNUM]; /*二维数组，表示边的邻接矩阵*/
}graph;

使用邻接矩阵的好处就在于增减边的操作简单，置 `A[i][i]` 为1或0就行，但缺点就在于增减顶点的操作需搬移大量元素，而且大多数情况下会造成存储空间的浪费（稀疏矩阵）。

2.2 邻接表

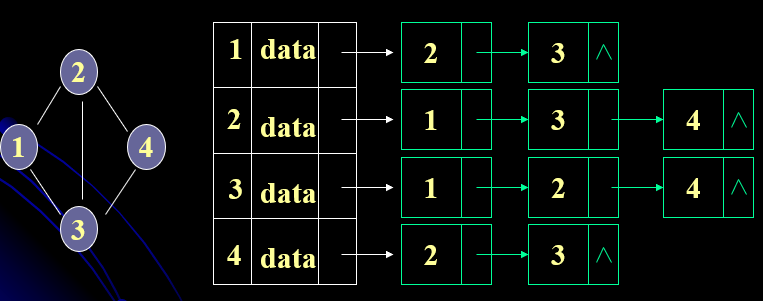
除了使用邻接矩阵，我们还可以使用邻接链表来构造图。在邻接链表中存在两种结点类型。如上图所示，头结点 定义了头结点编号、头结点值和一个指向与该头结点相邻的结点的指针；邻接结点 则定义了邻接结点编号和一个指向下一个与该头结点相邻的结点的指针。通过这样的方式存储图，优点在于节省存储空间，且边的插入和删除操作比较简便。